ОДЗ:
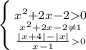
Решаем каждое неравенство:
 ⇒
⇒ 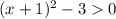 ⇒
⇒

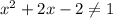 ⇒
⇒  ⇒
⇒ 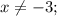
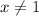

Подмодульные выражения обращаются в 0 в точках
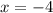 и
и 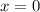
Это точки делят числовую прямую на три промежутка.
Раскрываем знак модуля на промежутках:
(-∞;-4]
|x+4|=-x-4
|x|=-x
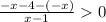 ⇒
⇒  ⇒ x < 1
⇒ x < 1
решение неравенства (-∞;-4]
(-4;0]
|x+4|=x+4
|x|=-x
 ⇒
⇒  ⇒ x < -2 или x > 1
⇒ x < -2 или x > 1
решение неравенства (-4;-2)
(0;+∞)
|x+4|=x+4
|x|=x
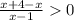 ⇒
⇒  ⇒ x > 1
⇒ x > 1
решение неравенства (1;+∞]
Объединяем ответы трех случаев:
 при
при 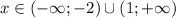
ОДЗ:

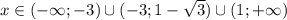
Решаем неравенство: 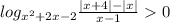
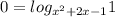
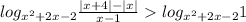
Два случая:
если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента
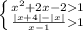 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.](/tpl/images/1360/8793/82812.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
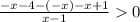 ⇒
⇒  ⇒
⇒ 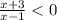 ⇒ (-3;-1)
⇒ (-3;-1)
не принадлежат (-∞;-4]
на (-4;0]
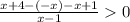 ⇒
⇒ 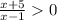 ⇒ x < -5 или x > 1
⇒ x < -5 или x > 1
не принадлежат (-4;0]
(0;+∞)
 ⇒
⇒ 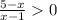 ⇒
⇒ 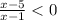 ⇒
⇒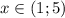
о т в е т этого случая 
если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента
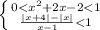 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.](/tpl/images/1360/8793/ac205.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
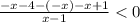 ⇒
⇒ 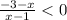 ⇒
⇒ 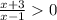 ⇒
⇒
(-∞;-3)U(1;+∞)
о т в е т. (-∞;-4]
на (-4;0]
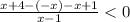 ⇒
⇒ 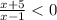 ⇒ -5 < x < 1
⇒ -5 < x < 1
о т в е т. (-4;0]
(0;+∞)
 ⇒
⇒ 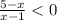 ⇒
⇒ 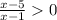 ⇒
⇒
о т в е т этого случая 
С учетом ОДЗ получаем окончательный ответ: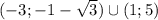
Объяснение:
Разложим на множители выражение в числителе и знаменателе.
\begin{gathered}y=\frac{24-12x}{2x-x^2}\\y=\frac{-12(x-2)}{-x(x-2)}\\\left \{ {{y=\frac{12}{x} } \atop {x\neq 2}} \right.\end{gathered}
y=
2x−x
2
24−12x
y=
−x(x−2)
−12(x−2)
{
x
=2
y=
x
12
Это гипербола, которая лежит в 1 и 3 четверти и имеет асимптоты, которыми являются оси координат.
Отметим 2 точки, которые принадлежат этой функции на координатной плоскости для более точно построения.
x=12 --> y=1; (12;1)
x=1 --> y=12; (1;12)
И проведём через них нашу гиперболу.
а) Пусть х - ширина, х+4 - длина. Периметр - 28 см. Составим уравнение:
х+х+х+4+х+4=28,
4х+8=28,
4х=28-8,
4х=20,
х=20/4,
х=5 (см) - ширина
5+4=9 (см) - длина
ответ: 5 см - ширина, 9 см - длина.
б) Пусть х - ширина, 3х - длина. Периметр - 24 см. Составим уравнение:
3х+3х+х+х=24,
8х=24,
х=24/8,
х=3 (см) - ширина
3*3=9 (см) - длина
ответ: ширина - 3 см, длина - 9 см.