1. 1 ОДЗ х∈(-∞;+∞), т.к. дан многочлен.
2. с осью ох. у=0, х³-3х²+4=0, х=2, делим х³-3х²+4 на х-2, получаем
(х²-х-2)=(х+1)(х-2), чтобы разложить на множители, предварительно по теореме, обратной теореме Виета, угадали корни, это -1 и 2, итак, точек пересечения с осью ох найдено две (-1;0);(2;0). с осью оу х=0, тогда у=4, точка (0;4)
3. вертикальных нет, наклонные проверим к= предел при х, стремящемся к ∞ f(x)/x равен бесконечности, поэтому нет и наклонных асимптот.
4. y(-x)=-x³-3x²+4 ≠y(x) не является четной, y(-x)≠ -y(x) не является нечетной. это функция общего вида.
5.находим производную и точки экстремума и интервалы монотонности. у'=3х²-6х=0 зх*(х-2)=0; х=0;х=2, исследуя знак производной, получаем, что функция убывает на промежутке [0; 2] и возрастает на каждом из промежутков (-∞;0] и [2;+∞)
___02
+ - + точка х=0- точка максимума, х=2- точка минимума
6.находим вторую производную. 6х-6=0, точка х=1 точка перегиба, т.к. при переходе через нее вторая производная меняет знак с минуса на плюс. 1
- +
На промежутке (-∞;1) график функции выпуклый вверх, а на промежутке (1;+∞) вниз.
Найти стороны прямоугольника.
Стороны прямоугольника обозначим через "х" и "у" .
Периметр прямоугольника равен Р=2(х+у)=160 ⇒ х+у=80 .
Когда увеличили одну сторону (пусть это будет сторона "х") на 40%, то есть на 0,4 части, то она стала равна (1+0,4)*х=1,4х .
Когда уменьшили вторую сторону на 40%, то есть на 0,4 части, то сторона стала равной (1-0,4)*у=0,6у .
Периметр такого прямоугольника уменьшился на 10%, то есть на 0,1 части, и стал равным (1-0,1)*Р=0,9*160=144 .
Теперь периметр прямоугольника равен 2(1,4х+0,6у)=144 ⇒
1,4х+0,6у=72 .
Решаем систему:
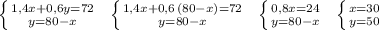
Стороны первого прямоугольника равны 30 см и 50 см, а стороны изменённого прямоугольника равны 1,4*30=42 см и 0,6*50=30 см .
Х=1
У=10
ответ: (1;10)