3sin^2(2x) + 10sin(2x) + 3 = 0.
Введем новую переменную, пусть sin(2x) = а.
Получается уравнение 3а^2 + 10а + 3 = 0.
Решаем квадратное уравнение с дискриминанта:
a = 3; b = 10; c = 3;
D = b^2 - 4ac; D = 10^2 - 4 * 3 * 3 = 100 - 36 = 64 (√D = 8);
x = (-b ± √D)/2a;
а1 = (-10 - 8)/(2 * 3) = -18/6 = -3.
а2 = (-10 + 8)/6 = -2/6 = -1/3.
Возвращаемся к замене sin(2x) = а.
1) sin(2x) = -3 (не может быть, синус любого угла больше -1, но меньше 1).
2) sin(2x) = -1/3.
Отсюда 2х = ((-1)^n * arcsin(-1/3))/2 + П/2 * n, n - целое число.
Делим все на 2: х = ((-1)^n * arcsin(-1/3))/2 + П/2 * n, n - целое число.
Предположим, что х часов - это время работы первой бригады, тогда (х+4) часа - время работы второй бригады, примем всю работу за 1
согласно этим данным составим и решим уравнение для совместной работы:
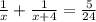 /·24x(x+4)
/·24x(x+4)
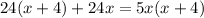
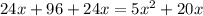
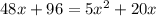
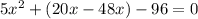
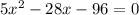
Cчитаем дискриминант:
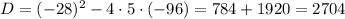
Дискриминант положительный
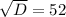
Уравнение имеет два различных корня:
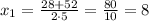
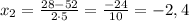
не удовлетворяет условию задачи, так как отрицательное время быть не может
х=8 (ч) - I бригада.
х+4=8+4=12 (ч) - II бригада.
Следовательно, первая бригада заасфальтирует участок дороги за 8 часов, а вторая за 12 часов.
Если у данного уравнения существуют два различных натуральных корня X1 и X2 , то их сумма и произведение - тоже натуральные числа. тогда по теореме Виета:
x_{1} *x_{2} = \frac{3a-5}{a} \\
\frac{3a-5}{a} = n_{1} , где n1 - нат. число. Тогда
3a-5 = n_{1}*a \\
Правая часть данного равенства делится на a, значит и левая должна тоже делиться на a. Слева имеем сумму двух слагаемых, чтобы это сумма делилась на a, надо чтобы оба слагаемых делились на a.
3a делится на а, и 5 должно делиться на а. Т.о. а∈{ -5, -1, 1, 5}.
Подставляем поочередно эти значения а в выражение \frac{3a-5}{a} .
a=-5, \frac{3*(-5)-5}{-5}= \frac{-20}{-5}= 4 \\ a=-1, \frac{3*(-1)-5}{-1}= \frac{-8}{-1}= 8 \\ a=1, \frac{3*1-5}{1}= \frac{-2}{1}= -2 \\ a=5, \frac{3*5-5}{5}= \frac{10}{5}= 2 \\
Т.о. натуральное значение выражение принимает при а=-5, а=-1 и а=5.
По т.Виета x_{1} + x_{2} = \frac{a^2+5}{a} \\
Проверим при каких из этих значений сумма корней исходного уравнения будет натуральным числом:
a=-5; \frac{(-5)^2+5}{-5} = \frac{30}{-5} = -6 \\ a=-1; \frac{(-1)^2+5}{-1} = \frac{6}{-1} = -6 \\ a=5; \frac{5^2+5}{5} = \frac{30}{5} = 6 \\
Итак, уравнение может иметь два различных натуральных корня только при a=5. Проверим будут ли этом значении а корни исходного уравнения натуральными числами.
При a=5. уравнение примет вид:
5 x^{2} - 30x +10 =0 \\ x^{2} - 6x +2 =0 \\ D = 28
значит корни будут иррациональными.
ответ: ∅.