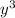 куб числа по модулю
куб числа по модулю 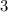 (остатки от деления) сравнимы с
(остатки от деления) сравнимы с 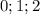 соответственно когда
соответственно когда 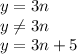 , где
, где 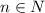 .
. 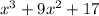
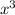 так же как
так же как 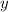 ,
,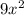 дает остаток
дает остаток 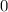 , число
, число 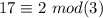 , то есть остаток числа
, то есть остаток числа 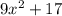 равен
равен 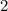 при делений на
при делений на 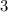 .
.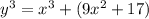
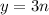 слева остаток всегда равен
слева остаток всегда равен 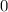 , но справа уже не может поэтому
, но справа уже не может поэтому 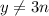
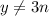 , слева остаток при делений на
, слева остаток при делений на 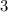 как ранее был сказан равен
как ранее был сказан равен  , но тогда справа должно быть число дающее
, но тогда справа должно быть число дающее 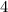 , а оно дает при делений на
, а оно дает при делений на 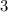 остаток
остаток  отсюда
отсюда 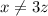 подходит
подходит 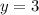
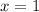
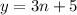 , но оно так же не действительно , то есть решение
, но оно так же не действительно , то есть решение 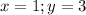
(х+1)^2=(-sqrt(x+1))^2
(x+1)^2=(x+1)
x^2+2x-1=x+1
X^2+x=0
x(x+1)=0
x1=0; x2=-1