Алгебра: Выражение 1-2sinx^2/sinx+cosx + sinx

Выражение 1-2sinx^2/sinx+cosx + sinx

👇

Ответ:

dreygar

18.09.2021

(1-2sin²x)/(sinx+cosx)+sinx=(cos²x-sin²x)/(sinx+cosx) +sinx=
=(cosx-sinx)(cosx+sinx)/(sinx+cosx) +sinx=cosx-sinx+sinx=cosx

4,4(5 оценок)

Открыть все ответы

Ответ:

Zikeev2007

18.09.2021

$\sqrt[5]{32a^7} \cdot \sqrt[5]{a^3} = 2\sqrt[5]{a^7} \cdot a^{\frac{3}{5}} = 2a^{\frac{7}{5}} \cdot a^{\frac{3}{5}} = 2a^{\frac{7}{5} + \frac{3}{5}} = 2a^{\frac{10}{5}} = \boxed{2a^2}$ .

ответ: В.

$\dfrac{1}{3}\sqrt[3]{-147} \cdot \sqrt[3]{-63} = \dfrac{1}{3}\cdot (-\sqrt[3]{147})\cdot (-\sqrt[3]{63}) = \dfrac{1}{3}\sqrt[3]{147\cdot 63} = \dfrac{\sqrt[3]{9261}}{3} = \dfrac{21}{3} =\\\\\\= \boxed{\textbf{7}}$

ответ: А.

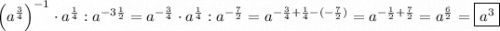
$\left (a^{\frac{3}{4}}\right )^{-1} \cdot a^{\frac{1}{4}} : a^{-3\frac{1}{2}} = a^{-\frac{3}{4}} \cdot a^{\frac{1}{4}} : a^{-\frac{7}{2}} = a^{-\frac{3}{4} + \frac{1}{4} - (-\frac{7}{2})} = a^{-\frac{1}{2} + \frac{7}{2}} = a^{\frac{6}{2}} = \boxed{a^3}$

ответ: Г.

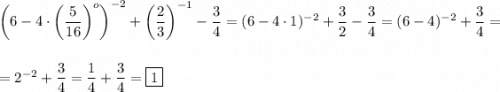
$\left (6 - 4\cdot \left(\dfrac{5}{16}\right )^o\right )^{-2} + \left (\dfrac{2}{3}\right )^{-1} - \dfrac{3}{4} = (6-4\cdot 1)^{-2} + \dfrac{3}{2} - \dfrac{3}{4} = (6-4)^{-2} + \dfrac{3}{4} =\\\\\\= 2^{-2} + \dfrac{3}{4} = \dfrac{1}{4} + \dfrac{3}{4} = \boxed{1}$

ответ: А.

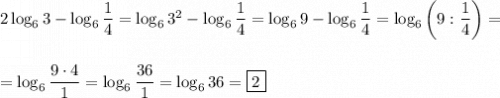
$2\log_{6}3 - \log_{6}\dfrac{1}{4} = \log_{6}3^2 - \log_{6}\dfrac{1}{4} = \log_{6}9 - \log_{6}\dfrac{1}{4} = \log_{6}\left (9 : \dfrac{1}{4}\right ) =\\\\\\= \log_{6}\dfrac{9\cdot 4}{1} = \log_{6}\dfrac{36}{1} = \log_{6}36 = \boxed{2}$

ответ: А.

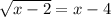
$\sqrt{x-2} = x-4$

Для начала решим систему неравенств, определяющую область допустимых значений :

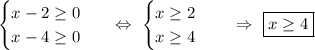
$\begin{equation*}\begin{cases}x - 2\geq 0\\x - 4\geq 0\end{cases}\end{equation*}\ \ \ \Leftrightarrow\ \begin{equation*}\begin{cases}x \geq 2\\x \geq 4\end{cases}\end{equation*}\ \ \ \ \Rightarrow\ \boxed{x\geq 4}$

Возводим обе части уравнения в квадрат.

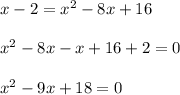
$x - 2 = x^2 - 8x + 16\\\\x^2 - 8x - x + 16 + 2 = 0\\\\x^2 - 9x + 18 = 0$

По теореме Виета:

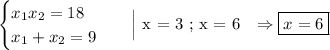
$\begin{equation*}\begin{cases}x_{1}x_{2} = 18\\x_{1}+x_{2} = 9\end{cases}\end{equation*}\ \ \ \Big| x = 3 ; x = 6\ \ \ \Rightarrow \boxed{x=6}$

3 не подходит под область допустимых значений.

ответ: корень только один, и он положительный.

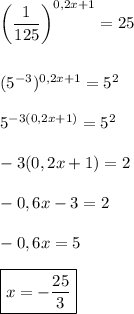
$\left (\dfrac{1}{125}\right )^{0,2x+1} = 25\\\\\\(5^{-3})^{0,2x+1} = 5^2\\\\5^{-3(0,2x+1)} = 5^2\\\\-3(0,2x+1) = 2\\\\-0,6x - 3 = 2\\\\-0,6x = 5\\\\\boxed{x = -\dfrac{25}{3}}$

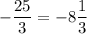$-\dfrac{25}{3} = -8\dfrac{1}{3}$ , тогда корень принадлежит промежутку (-9; -7] .

ответ: (-9; -7] .

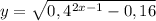
$y = \sqrt{0,4^{2x-1} - 0,16}$

Областью определения функции является решение следующего неравенства:

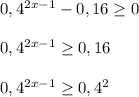
$0,4^{2x-1} - 0,16 \geq 0\\\\0,4^{2x-1} \geq 0,16\\\\0,4^{2x-1} \geq 0,4^2$

Так как основание меньше единицы, то:

$2x - 1\leq 2\\\\2x \leq 3\\\\x \leq 1,5\ \ \ \ \Rightarrow \boxed{x\in(-\infty; 1,5]}$

ответ: $(-\infty; 1,5]$ .

Найдём область значения функции. 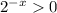$2^{-x} 0$ , тогда 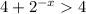$4+2^{-x} 4$ . Значит, 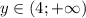$y \in (4; +\infty)$ . Следовательно, из перечисленных чисел в множество значений входит только 5 (4 не входит, так как концы не включаем).

ответ: 5.

10)

Условие чётности функции: 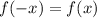f(-x) = f(x) . Проверяем для каждой.

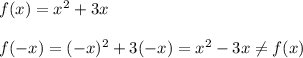$f(x) = x^2 + 3x\\\\f(-x) = (-x)^2 + 3(-x) = x^2 - 3x \neq f(x)$ - не подходит.

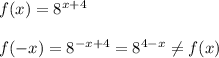$f(x) = 8^{x+4}\\\\f(-x) = 8^{-x+4} = 8^{4-x} \neq f(x)$ - не подходит.

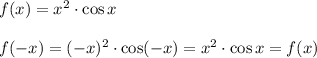$f(x) = x^2\cdot \cos x\\\\f(-x) = (-x)^2 \cdot \cos(-x) = x^2 \cdot \cos x = f(x)$ - подходит.

ответ: 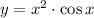$y = x^2\cdot \cos x$ .

4,5(49 оценок)

Ответ:

danik131

18.09.2021

Объяснение:

учимся проговаривать формулы сокращенного выражения:

Разность квадратов двух выражений равна произведению их разности и их суммы.

Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.

Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.

Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.

Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.