3sin^2(2x) + 10sin(2x) + 3 = 0.
Введем новую переменную, пусть sin(2x) = а.
Получается уравнение 3а^2 + 10а + 3 = 0.
Решаем квадратное уравнение с дискриминанта:
a = 3; b = 10; c = 3;
D = b^2 - 4ac; D = 10^2 - 4 * 3 * 3 = 100 - 36 = 64 (√D = 8);
x = (-b ± √D)/2a;
а1 = (-10 - 8)/(2 * 3) = -18/6 = -3.
а2 = (-10 + 8)/6 = -2/6 = -1/3.
Возвращаемся к замене sin(2x) = а.
1) sin(2x) = -3 (не может быть, синус любого угла больше -1, но меньше 1).
2) sin(2x) = -1/3.
Отсюда 2х = ((-1)^n * arcsin(-1/3))/2 + П/2 * n, n - целое число.
Делим все на 2: х = ((-1)^n * arcsin(-1/3))/2 + П/2 * n, n - целое число.
Предположим, что х часов - это время работы первой бригады, тогда (х+4) часа - время работы второй бригады, примем всю работу за 1
согласно этим данным составим и решим уравнение для совместной работы:
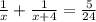 /·24x(x+4)
/·24x(x+4)
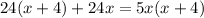
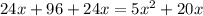
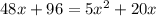
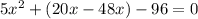
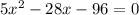
Cчитаем дискриминант:
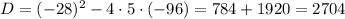
Дискриминант положительный
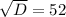
Уравнение имеет два различных корня:
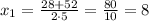
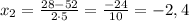
не удовлетворяет условию задачи, так как отрицательное время быть не может
х=8 (ч) - I бригада.
х+4=8+4=12 (ч) - II бригада.
Следовательно, первая бригада заасфальтирует участок дороги за 8 часов, а вторая за 12 часов.
Решение. Перепишем ребус столбиком:
Ясно, что первая цифра суммы Д = 1, так как сумма двух четырехзначных чисел не может превышать 19999. Ребус приобретает такой вид:
Третья цифра суммы А равна либо 2, либо 3. Однако, цифра А стоит в конце суммы и получается от сложения двух равных чисел Р. Значит, А – четная цифра, она не 3, а 2. Снова перепишем ребус:
Сумма Р + Р может дать на конце двойку в двух случаях: при Р = 1 и при Р = 6. Однако, Р = 1 невозможно, поскольку Д = 1. Значит, Р = 6, К = 5, а У либо 3, либо 8. Но так как сумма пятизначная, то У = 8.
ответ: 8126 + 8126 = 16252.
125. Попытайся понять, как составлена эта последовательность, и продолжи ее: 1, 2, 6, 24, 120, 720.
Решение. Второе число получается из первого умножением на 2, третье из второго умножением на 3 и т. д.
ответ: 1, 2, 6, 24, 120, 720, 5040, ...
126. По круговой беговой дорожке длиной 400 м бегут Андрей и Виктор. Андрей бежит быстрее и обгоняет Виктора через каждые 12 минут. Через 36 минут после начала бег был прекращен. Кто пробежал больше и на сколько?
Решение. Андрей пробежал больше, чем Виктор, так как бежал то же время с большей скоростью. За каждые 12 минут Андрей пробегает на 1 круг больше, чем Виктор. Значит, за 36 минут Андрей пробежал на 3 круга больше, а три круга – это 1200 м.
ответ: Андрей пробежал больше на 1200 м.
127. Сумма и произведение четырех чисел равны 8. Что это за числа?
Решение. Осуществляется подбором:
1 + 1 + 2 + 4 = 1 x 1 x 2 x 4
ответ: 1, 1, 2 и 4.