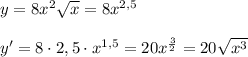
1.1) arcsin(-1) + arccos0 = π + (π/2) = 3π/2
Пусть arcsin(-1) = α, тогда cosα = -1, значит α = π
Пусть arccos0 = β, тогда cosβ = 0, значит β = (π/2)
2) arctg + arctg(- √3) = π/4 + (-π/3) = 1
2. x=±arccosa+2πk,k∈Z .
3.tg(2x) = 2·tg(x)/(1 - tg²(x))
4.cos 5x-cos 7x=0
-2sin 6x*sin (-x)=0(-2 на синус полусуммы углов умножить на синус полуразности углов)
sin 6x=0 или sin x=0
6x=pn, x=pn/6 или x=pn
x=pn/6
5. sin (3x) =1
3х= π/2+2πn
x= π/6 + (2πn)/3
7. sin(3x)-sin(x)=0
2*sin((3x-x)/2)*cos((3x+x)/2)=0
2sin(x)*cos(2x)=0
1) sin(x)=0
x=π*n
2) cos(2x)=0
2x=(pi/2)+pi*n
x=(pi/4)+pi*n/2
Объяснение:
Итак, мы имеем дело с алгебраической дробью.
Давайте мы упростим числитель и знаменатель данной дроби.
Числитель:
10a^2 можно разложить на множители - 2 * 5 * a * a
25ab можно тоже разложить на множители - 5 * 5 * a * b
Знаменатель:
b можно вынести за скобку.
И в итоге все это выглядит так:
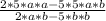
А теперь посмотрим в числитель дроби:
5a можно вынести за скобку, так как это число есть у обоих слагаемых.
А в знаменателе b вынесем за скобку по выше сказанной причине.
Получаем:
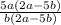
Мы числитель и знаменатель можем сократить на (2a-5b).
И в итоге получаем результат:
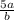
Подставляем данные нам значения в дробь:
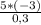
Получаем -15/0,3 = -150/3 = -50
ответ: -50
Задача решена.