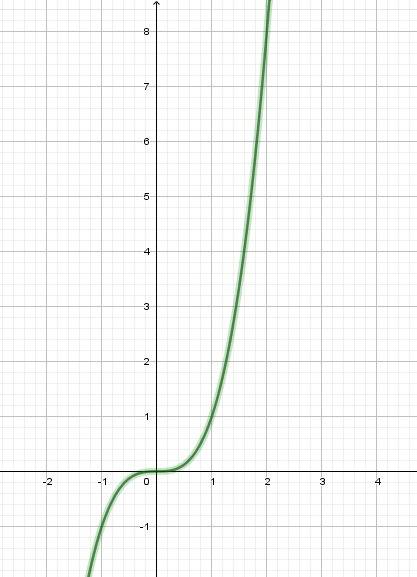
Точки построения графика: (0;0), (±1; ±1), (±2; ±8). График является нечетной.
Подставим координаты точки A(-5;125) в график уравнения, получим
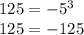
Поскольку равенство не верно, то график функции y = x³ не проходит через точку A(-5;125), т.е. точка не принадлежит графику y = x³
Подставим теперь координаты точки B(4;64), получим
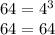
Поскольку равенство тождественно выполняется, то точка B принадлежит графику функции y = x³.
Подставим координаты точки C(-3;-27), имеем
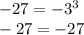
Раз равенство тождественно выполняется, то точка C(-3;-27) принадлежит графику функции y = x³
sin^2(a+b)+cos^2(a-b)-sin2a sin2b=
=(1-cos(2a+2b))/2+(1+cos(2a-2b))/2-sin2asin2b=
=1/2-1/2cos2acos2b+1/2sin2asin2b+1/2+1/2cos2acos2b+1/2sin2asin2b-
sin2asin2b=2
2
а) sin(179°+x) cos x -cos(179°+x) sin x>0
sin(179+x-x)>0
sin179>0
x∈(-∞;∞)
б)x^2-2x cos6,5 cos0,5+cos6 cos7<0
cos6,5cos0,5=1/2(cos(6,5-0,5)+cos(6,5+0,5))=1/2(cos6+cos7)
x²-2x*1/2(cos6+cos7)+cos6cos7<0
x²-x(cos6+cos7)+cos6cos7<0
x1+x2=cos6+cos7 U x1*x2=cos6cos7
x1=cos6 U x2=cos7
x∈(cos6;cos7)