![\left \{ {{(x-2)^2 \leq (2x+3)^2-8(x+5)} \atop {x^2+x-42\ \textless \ 0}} \right. \\\\1)\; \; x^2-4x+4 \leq 4x^2+12x+9-8x-40\\\\3x^2+8x-35 \leq 0\\\\D/4=121\; ,\; \; x_1=-5,\; \; x_2=\frac{7}{3}=2\frac{1}{3}\\\\3(x+5)(x-\frac{7}{3} )\leq 0\qquad +++[-5\, ]---[\frac{7}{3}\, ]+++\\\\x\in [-5;\frac{7}{3}\, ]\\\\2)\; \; x^2+x-42\ \textless \ 0\\\\x_1=-6,\; \; x_2=7\; \; (teorema\; Vieta)\\\\(x+6)(x-7)\ \textless \ 0\qquad +++(-6)---(7)++\\\\x\in (-6,7)](/tpl/images/0634/5972/e5ff5.png)
![3)\quad \left \{ {{x\in [-5,\, 2\frac{1}{3}\, ]} \atop {x\in (-6,7)}} \right. \quad \Rightarrow](/tpl/images/0634/5972/b82c4.png)
![x\in [-5\, ;\, 2\frac{1}{3}\, ]](/tpl/images/0634/5972/f3160.png)
По условию скорость мотоциклиста больше скорости велосипедиста, значит,
10 км - это расстояние, которое проехал велосипедист до встречи;
тогда
50-10=40 км - это расстояние, которое проехал мотоциклист до встречи.
Пусть х км/ч - скорость велосипедиста, тогда
(х+30) км/ч - скорость мотоциклиста;
10/х ч - время движения велосипедиста до встречи;
40/(х+30) ч - время движения мотоциклиста до встречи.
По условию на движение до встречи каждый из них потратил одинаковое количество времени, получаем уравнение:

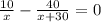
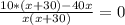
ОДЗ: x>0
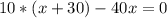



10 км/ч - скорость велосипедиста,
S v t
туда 24 км x 24 : x
обратно 24 км x+2 24: (x+2)
24/x - 24/x+2 = 2
24x + ( 24+24) - 24x = 2x во 2 степени + 4x
х во 2 степени + х2 - 24 = 0
2x во 2 степени + 4х - 48 = 0
х в 1 степени = 6 не подходит
х во 2 степени = 4
4+2= 6 км в час