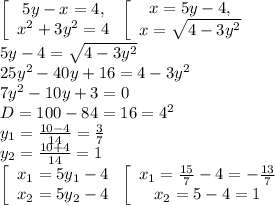
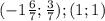
по моему не существует метода добавления, решу подстановкой.
1) выразим х из 1 уравнения:
х= (5у-30)\2
2) подставляем во 2 уравнение вместо х получившееся:
3* (5у-30)\2- 8у+52=0
подгоняем все под знаменатель 2:
(15у-90-16у+104)\2=0
дробь рана 0, когда ее числитель равен 0, а знаменатель не равен. значит отбрасываем знаменатель. НО. на 0 делить нельзя, значит нельзя, чтобы в знаменателе получился 0. но тут нас устроят любые значения у, тк у нет в знаменателе. решаем:
-у+14=0
у=14.
3) подставляем вместо у 14 в 1 уравнение:
2х-70= -30
2х= 40
х=20
ответ: 20, 14
решу систему методом подстановки.
1) выразим х через второе уравнение:
х= (5-7у)\3
2) подставляешь в 1 уравнение вместо х получившееся выражение:
4* (5-7у)\3 -5у=-22
(20-28у)\3-5у=-22
перегоним все в левую часть:
(20-28у)\3-5у+22=0
подгоним все под общий знаменатель 3:
(20-28у-15у+66)\3=0
3) дробь равна 0, когда числитель равен 0, а знаменатель не равен. значит отбрасываем знаменатель. НО. на 0 делить нельзя, значит нельзя, чтобы в знаменателе получился 0. но тут нас устроит любое значение х, тк х нет в знаменателе. решаем:
-43у+86=0
43у= 86
у= 86\43
4) подставляем во 2 уравнение вместо у получившееся:
3х+ 7* 86\43=5
3х+ 608\43-5=0
подгоняем под общий знаменатель:
(129х+608-215)\43=0
тоже самое, что и в 3 действии:
129х= -393
х= - 393\129= -131\43
X^2 + 3y^2 = 4
••••••
X = 5y - 4
( 5y - 4 )^2 + 3y^2 = 4
25y^2 - 40y + 16 + 3y^2 - 4 = 0
28y^2 - 40y + 12 = 0
4( 7y^2 - 10y + 3 ) = 0
D = 100 - 84 = 16 = 4^2
y1 = ( 10 + 4 ) : 14 = 1
y2 = ( 10 - 6 ) : 14 = 2/7
X = 5y - 4
X1 = 5•1 - 4 = 1
X2 = 5•( 2/7 ) - 4 = ( 10/7 ) - 4 = 1 3/7 - 3 7/7 = - 2 4/7
ответ ( 1 ; 1 ) ; ( - 2 4/7 ; 2/7 )