10sin^2x-17cosx-16=0
10(1-cos^2x)-17 cosx-16=0 (основное тригонометрическое тождество)
10-10cos^2x-17cosx-16=0
-10cos^2x-17cosx-6=0
10cos^2x+17cosx+6=0
Мы привели к простому квадратному уравнению.
Введём замену: cos x=t
10t^2+17t+6=0
10t^2+5t+12t+6=0
(5t+6)(2t+1)=0
t=-6/5
t=-1/2
Из этого получаем следующую совокупность:
cosx=-6/5 => нет решений, т.к. cos a ≥ -1
cosx=-1/2 => x=60°, или π/3 радиан.
ответ: π/3.
Если вам понравилось решение, ставьте большие пальцы вверх,жмите сердца, подписывайтесь на канал, сохраняйте видос и до скорых встреч в эфире deyvarFM.
Одночлены можно сложить с приведением подобных членов в случае, если буквенная часть одинакова, а коэффициенты (числовые множители перед буквенной частью ) различные.
Действуем по правилу сложения подобных слагаемых. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, из того, что написано:
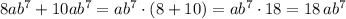 ,
,
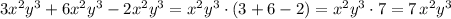 .
.
Если одночлены не подобны, то упрощение суммы не получится, а останется многочлен, то есть сумма нескольких одночленов. Например, сумма одночленов
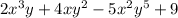 не может быть упрощена, так как буквенные части одночленов различны.
не может быть упрощена, так как буквенные части одночленов различны.
А вот пример, где можно немного упростить сумму одночленов.
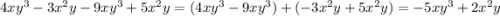 .
.
F`(x)=[16x*4x-4*(8x²+1)]/16x²=(64x²-32x²-4)/16x²=(32x²-4)/16x²=0
4(8x²-1)=0
4(2√2x-1)(2√2x+1)=0
x=1/2√2 x=-1/2√2
+ _ +
(-1/2√2)(1/2√2)
max min
ymax=(8*1/8+1):(4*1/2√2)=2:√2=√2
ymin=(8*1/8+1);(-4*1/2√2)=2:(-√2)=-√2
F(x)=(x^2 -x+4)//x^2+4 [0;+∞)
F`(x)=[(2x-1)*(x²+4)-2x*(x²-x+4)]/(x²+4)²=
=(2x³+8x-x²-4-2x³+2x²-8x)/(x²+4)²=(x²-4)/(x²+4)²=0
(x-2)(x+2)=0
x=2 x=-2
+ _ +
(-2)[0](2)
min
ymin=(4-2+4)/(4+4)=6/8=3/4
F(x)=(x^2 -5x+6)//x^2 +1 (-∞;0]
F`(x)=[(2x-5)(x²+1)-2x(x²-5x+6)]/(x²+1)²=
=(2x³+2x-5x²-5-2x³+10x²-12x)/(x²+1)²=(5x²-10x-5)/(x²+4)²=0
5(x²-2x-1)=0
D=4+4=8
x1=(2-2√2)/2=1-√2 U x2=1+√2
+ _ +
(1-√2)[0](1+√2)
max
ymax=[(1-√2)²-5(1-√2)+6)]/[(1-√2)²+1]=(1-2√2+2-5+5√2+6)/(1-2√2+2+1)=
=(4+3√2)/(4-2√2)=(4+3√2)(4+2√2)/(16-8)=(16+20√2+12)/8=(28+20√2)/8=
=(7+5√2)/2