а - длина прямоугольника
b - ширина прямоугольника
=================================================================
Р=28 м
S=40 м²
а - ? м
b - ? м
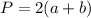 (1)
(1)
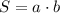 (2)
(2)
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
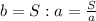
подставляем в формулу периметра прямоугольника (1)
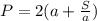
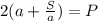
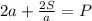
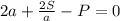 /·a
/·a
умножаем на а для того, чтобы избавится от знаменателя
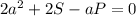
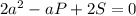
подставим в уравнение данные P и S
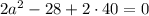
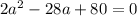
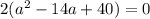
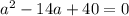
Квадратное уравнение имеет вид:
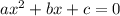
Cчитаем дискриминант:
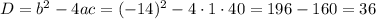
Дискриминант положительный
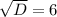
Уравнение имеет два различных корня:
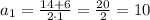
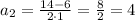
Следовательно стороны равны 10м и 4м соответственно
ответ: 10м и 4м стороны прямоугольника.
Проверка:
Р=2(а+b)=2(10+4)=2·14=28 (м)
S=a·b=10·4=40 (м²)
1200 = 2*2*2*2*3*5*5
16 = 2*2*2*2
50 = 2*5*5
значит а = 3 * (любое число которое можно скомбинировать из произведения четерых 2 и произведения двух 5).
подщитаем количество этих комбинаций.
комбинаций для двоек есть 5 штук: нету двоек, 1двойка. 2 двойки..4 двойки
комбинация для пятерок 3 штуки:нету пятерок, 1 петерка 2 петярки.
значит всего чисел будет 5*3, тоесть 15
чтоб было понятно, чисола "а" могут быть такими
^ - это значек степени
3 * (2^0 * 5^0)
3 * (2^1 * 5^0)
3 * (2^2 * 5^0)
3 * (2^3 * 5^0)
3 * (2^4 * 5^0)
3 * (2^0 * 5^1)
3 * (2^1 * 5^1)
3 * (2^2 * 5^1)
3 * (2^3 * 5^1)
3 * (2^4 * 5^1)
3 * (2^0 * 5^2)
3 * (2^1 * 5^2)
3 * (2^2 * 5^2)
3 * (2^3 * 5^2)
3 * (2^4 * 5^2)
y=f'(x₀)(x-x₀)+f(x₀)
x₀=0,5
f(x₀)=0,75
f'(x)=(2x-x²)'=2-2x
f'(x₀)=2-2*0,5=2-1=1
Подставляем все найденные значения в уравнение касательной:
y=1*(x-0,5)+0,75=x-0,5+0,75=x+0,25
Площадь фигуры, ограниченной графиками функций находится по формуле:
S=∫(f(x)-g(x))dx
Верхний предел интегрирования будет равен 0,5 или 1/2 (точка касания прямой и параболы), а нижний предел интегрирования равен
x+0,25=0
x=-0,25=-1/4 (точка пересечения касательной с прямой y=0 или осью абсцисс)
Предлагаю начертить графики на координатной плоскости. Где сразу видны пределы интегрирования и график функции y=x+0,25 расположен выше графика функции y=2x-x². Записываем интеграл и решаем его: