5/9 и 1/3
Объяснение:
Пусть числитель дроби равен х, тогда её знаменатель равен х+4. Запишем первоначальную дробь х/(х+4)
Числитель дроби уменьшили на 3 и он стал равен х-3. Знаменатель дроби уменьшили на 3 и он стал равен х+4-3=х+1. Получили дробь (х-3)/(х+1).
По условию, полученная дробь на 2/9 меньше первоначальной. Составляем уравнение:
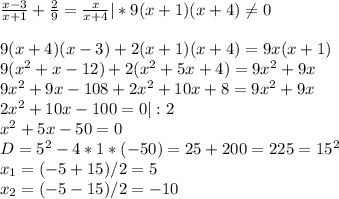
Итак, если х=5, то первоначальная дробь равна 5/(5+4)=5/9 - правильная дробь и полученная дробь равна (5-3)/(9-3)=2/6=1/3
Если х=-10, то первоначальная дробь равна -10/(-10+4)=-10/-6=5/3 - неправильная дробь, что противоречит условию.
Следовательно, получаем дроби 5/9 и 1/3
ответ: R=19 см.
Объяснение:
Пусть a и b - стороны прямоугольника. По условию, 2*(a+b)=57, откуда a+b=57/2 см. Допустим, что прямоугольник вращается вокруг своей стороны b, тогда радиус образовавшегося цилиндра R=a см, а его высота H=b=57/2-a=57/2-R см. Объём цилиндра V=π*R²*H=π*R²*(57/2-R)=57/2*π*R²-π*R³ см³. Производная V'(R)=57*π*R-3*π*R²=3*π*R*(19-R). Приравнивая её к нулю, получаем уравнение 3*π*R*(19-R)=0. Так как R≠0, то отсюда R=19 см - единственная критическая точка. Если R<19, то V'(R)>0, так что на интервале (0;19) функция V(R) возрастает. Если R>19, то V'(R)<0, так что на интервале (19;57/2) функция V(R) убывает (при R=57/2 V=0, а при R>57/2 V<0, что невозможно). Отсюда следует, что V(R) имеет максимум при R=19 см, этот максимум равен V(19)=π*19²*(57/2-19)=3429,5*π см³.
(а+b)(x-y)=ах-ау+bх-bу
(m-n)(p+q)=mp+mq-np-nq