4 км/час и 6 км/час
Объяснение:
пусть х км/час - скорость 1- го пешехода( х>0),
у км /час-скорость 2-го пешехода у>0)
(12/х) час-время в пути первого пешехода до встречи,
(12/ у) час-время в пути 2-го пешехода до встречи
по условию задачи известно, что первый был в пути на 1 час больше(в условии сказано, что один из них вышел на один час раньше второго. я выбрала , что это первый пешеход)
уравнение:
(12/ х)-(12/у)=1
по условию известно, что если бы пешеходы вышли одновременно, то встретились бы через 2 часа 24 минуты (144/60 час), тогда (х+у) км/час - скорость сближения
уравнение:
(х+у)*(144/60)=24
система уравнений:
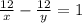
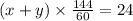
решить систему уравнений, получим х=4 км/час
у=6 км/час
Объяснение:
В основе метода математической индукции (ММИ) лежит принцип математической индукции: утверждение $P(n)$ (где $n$ - натуральное число) справедливо при $\forall n \in N$, если:
Утверждение $P(n)$ справедливо при $n=1$.
Для $\forall k \in N$ из справедливости $P(k)$ следует справедливость $P(k+1)$.
Доказательство с метода математической индукции проводится в два этапа:
База индукции (базис индукции). Проверяется истинность утверждения при $n=1$ (или любом другом подходящем значении $n$)
Индуктивный переход (шаг индукции). Считая, что справедливо утверждение $P(k)$ при $n=k$, проверяется истинность утверждения $P(k+1)$ при $n=k+1$.
Метод математической индукции применяется в разных типах задач:
Доказательство делимости и кратности
Доказательство равенств и тождеств
Задачи с последовательностями
Доказательство неравенств
Нахождение суммы и произведения
а) 3√3 = √9•3 = √27, 2√6 = √4•6 = √24, 4√2 = √16•2 = √32, 2√11 = √44, 2√6 < 3√3 < √29 < 4√2 < 2√11;
б) 6√2 = √36•2 = √72, 3√7 = √9•7 = √63, 2√14 = √4•14 = √56, 5√3 = 75, 2√14 < √58 < 3√7 < 6√2 < 5√3.