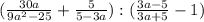
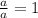, что 
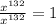, и что даже 
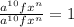. Выходит, что и 
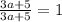. А теперь внимание на тот шаг, когда единицу мы представили в виде одинаковых значений для числителя и знаменателя, что и у знаменателя уменьшаемого числа. 
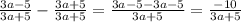, или равно 
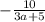. Что же, делитель стал выглядеть несколько изящнее, теперь разбираемся с делимым.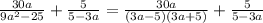 
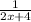равно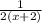 
, 
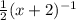и даже равно 
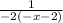, или равно 
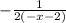, так? Выходит, что и 
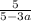равно 
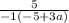, или равно 
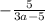. Однако не стоит забывать о том, что обыкновенные дроби нельзя складывать/вычитать, имея при этом разные знаменатели. Необходимо умножить числитель и знаменатель вычитаемого на 
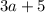, чтобы основания дробей обрели одинаковое значение: 
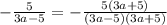. Теперь то можно складывать.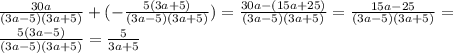 
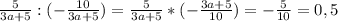
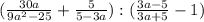равно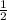 
при любом значении α.
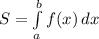. Пределы интегрирования можно определить по рисунку, а можно и аналитически решив уравнение: 4х-х²=0; x(4-x)=0; x=0; 4-x=0; x=4. То есть наша фигура расположена на промежутке [0;4]. Далее подставляем нашу функцию и пределы интегрирования в формулу площади и считаем: 
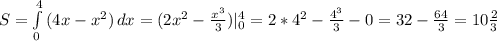ед².
10х-14=0
10х=14
х=1,4