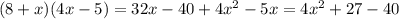
ответ:х км/год - швид. поїзда
(х+36)км/год - швид. авто
Відстань однакова
7х=3(х+36)
4х=108
х=27(км/год) - швидкість поїзда
27+36=63(км/год) - шв. автомобіля
40. Автомобіль їхав 3 години по шосе і 2 години – по
ґрунтовій дорозі, де його швидкість була на 15 км/год менше, ніж на шоссе. Всього
за 5 годин автомобіль проїхав 270 км. Знайдіть швидкість автомобіля на шоссе і на дорозі.
х км/год - швид. по шосе
(х-15) км/год - шв. по грун. дорозі
3х+2(х-15)=270
5х=300
х=60(км/год) - шв. по шосе
60-15=45(км/год) - швид. по грунт. дорозі
41. Автомобіль проїхав з пункту А до пункту В зі швидкістю 70 км/год. На
зворотному шляху він зменшив швидкість на 10 км/год і витратив на 45 хвилин
більше. Знайдіть відстань між А і В.
х год - час руху від А до В
(х-0,75) год - час руху від В до А
70х=60(х+0,75)
10х=45
х=4,5(год) - час руху від А до В
70*4,5=315(км) - відстань від А до В
42. Турист пройшов дві ділянки шляху протягом 12 годин.
На одній із ділянок він ішов зі швидкістю 4 км/год, а на іншій – 5 км/год.
Знайдіть довжину кожної ділянки, якщо середня швидкість туриста склала 4,75 км/год.
х год - час руху на І ділянці
(12-х) год - час руху на ІІ ділянці
4х+5(12-х)=4,75*12
4х+60-5х=57
х=3(год) - час руху на І ділянці
4*3=12(км) - довжина І ділянки
12-3=9(год) - час руху на ІІ ділянці
5*9=45(км) - довжина ІІ ділянки
43. Із двох пунктів, відстань між якими 2 км, одночасно
назустріч один одному вирушили пішохід і вершник. Яка швидкість кожного, якщо
вершник їхав на 12 км/год. швидше пішохода й вони зустрілися через 5 хв.?
5хв=1/12год
х км/год - шв пішохода
(х+12)км/год - шв вершника
2: 1/12=(х+х+12)
2х+12=24
2х=12
х=6(км/год) - шв. пішохода
6+12=18(км/год) - шв. вершника
44. З двох міст назустріч один одному одночасно виїхали
мотоцикл і легкова машина.Швидкість легкової машини дорівнює 56 км/год, що
становить QUOTE швидкості мотоцикла. Знайдіть відстань між
містами, якщо мотоцикл і машина зустрілись через 2 QUOTE год після початку руху.
№45., як 41
Воспользуемся леммой
Если m-простое число в данном случае m=37, то набор N={2,3,4,5...,35} всегда можно разбить на пары (a,b) произведении которых, будут давать a*b дает остаток 1 по модулю 37 (некий частный случай Теоремы Вильсона).
Преобразуем
1/2^2+2/3^2+3/4^2+...+35/36^2 = ((3*4*5*...*36)^2+2*(2*4*5*6*...*36)^2+...+35*(2*3*4*...*35)^2)/(36!)^2
По теореме Вильсона 36! = 36 по mod 37 значит докажем числитель делится на 37 (это и докажет что p делится на 37) так как q не делится на 37.
Воспользовавшись леммой, получаем что каждое слагаемое в числителе
(3*4*5*...*36)^2=(36*x1)^2 по mod 37
(2*4*5*6*...*36)^2=(36*x2)^2 по mod 37
(2*3*5*6*...*36)^2=(36*x3)^2 по mod 37
...
(2*3*4*5*...*35)^2=1 mod 37 (Теорема Вильсона)
Отметим что x1,x2,x3.,,,.x(m-3) чисел попарно различные, образующие очевидно множество {2,3,4,...m-2} тогда среди можно выбрать два элемента которые дадут сравнение x^2=y^2 mod 37 потому что (x-y)(x+y)=0 mod 37 , а множество можно разбить на соответственные суммы 2+35=3+34=...=18+19
p=36^2(1*x1^2+2*x2^2+3*x3^2+4*x4^2+...+34*x(34)^2)+35
так как 36^2=1 по mod 37
Докажем что (1*x1^2+2*x2^2+3*x3^2+4*x4^2+...+34*x(34)^2) = 2 mod 37
Так как выше было сказано что половина остатков равные, то выражение можно записать через остатки которые будут образовывать последовательную сумму (так как набор из множества {2,3,4,...,35} откуда
p=35*(2^2+3^2+4^2+...+17^2+18^2)
воспользуемся формулой что 1^2+2^2+3^2+...n^2=n(n+1)(2n+1)/6
Тогда p=35*(18*19*37/6-1) = 35*3*19*37 - 35 = 0-(37-2) = 2 mod 37
То есть p=36^2*2+35 = 1*2+35 = 0 mod 37