Решить логарифмическое неравенство log₅(1-3*x) < 2 желательно с объяснениями

👇

Увидеть ответ

Ответ:

Кимчи12

15.06.2020

㏒₅(1-3х)<2
1-3x<5²
1-3x<25
-3x<25-1
-3x<24
x>-8
ОДЗ 1-3х>0
-3x>-1
x<1/3
ответ:(-8;1/3)

4,8(74 оценок)

Ответ:

Макси00084322233

15.06.2020

ответ в приложении ♡♢♡♤■□□■■■
Решить логарифмическое неравенство log₅(1-3*x) < 2 желательно с объяснениями

4,8(4 оценок)

Открыть все ответы

Ответ:

Victoria0NK

15.06.2020

x∈(-∞; -0,25)∪(0; 0,5)

Объяснение:

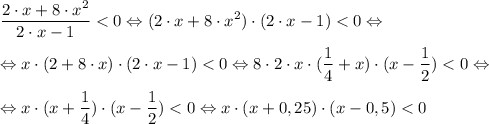
$\displaystyle \frac{2 \cdot x+8 \cdot x^{2}}{2 \cdot x-1}<0 \Leftrightarrow (2 \cdot x+8 \cdot x^{2})\cdot(2 \cdot x-1)<0 \Leftrightarrow \\\\\Leftrightarrow x \cdot (2 +8 \cdot x)\cdot (2 \cdot x-1)<0 \Leftrightarrow 8 \cdot 2 \cdot x \cdot (\frac{1}{4} + x)\cdot(x-\frac{1}{2})<0 \Leftrightarrow \\\\\Leftrightarrow x \cdot (x+\frac{1}{4}) \cdot (x-\frac{1}{2})<0 \Leftrightarrow x \cdot (x+0,25) \cdot (x-0,5)<0$

Рассмотрим функцию:

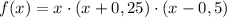
$\displaystyle f(x)=x \cdot (x+0,25) \cdot (x-0,5)$

Определим нули функции f(x):

f(x) =0 ⇔ x·(x+0,25)·(x-0,5)=0 ⇔ x₁= -0,25, x₂=0, x₃=0,5.

Нули функции f(x) делят делят ось Ох на промежутки (-∞; -0,25), (-0,25; 0), (0; 0,5) и (0,5; +∞), в каждом из которых функция f(x) сохраняет свой знак (применяем метод интервалов). Поэтому:

1) при x∈(-∞; -0,25) функция f(x)=x·(x+0,25)·(x-0,5)<0, так как, например при -0,5∈(-∞; -0,25):

f(-0,5)=(-0,5)·(-0,5+0,25)·(-0,5-0,5)=(-0,5)·(-0,25)·(-1)= -0,125<0;

2) при x∈(-0,25; 0) функция f(x)=x·(x+0,25)·(x-0,5)>0, так как, например при -0,05∈(-0,25; 0):

f(-0,05)=(-0,05)·(-0,05+0,25)·(-0,05-0,5)=(-0,05)·0,2·(-0,55)= 0,0055>0;

3) при x∈(0; 0,5) функция f(x)=x·(x+0,25)·(x-0,5)<0, так как, например при 0,05∈(0; 0,5):

f(0,05)=0,05·(0,05+0,25)·(0,05-0,5)=0,05·0,3·(-0,45)= -0,00675<0;

4) при x∈(0,5; +∞) функция f(x)=x·(x+0,25)·(x-0,5)>0, так как, например при 0,75∈(0,5; +∞):

f(0,75)=0,75·(0,75+0,25)·(0,75-0,5)=0,75·1·0,25= 0,1875>0;

Тогда решением заданного неравенства будет:

x∈(-∞; -0,25)∪(0; 0,5).

4,7(43 оценок)

Ответ:

prodaction2016

15.06.2020

Объем вычислительной работы будет значительно меньше, если порождать последовательность перестановок в порядке минимального изменения позиций элементов при переходе к каждой следующей перестановке. Для того, чтобы изменение было минимальным, любая перестановка должна отличаться от предыдущей транспозицией двух соседних (смежных) элементов. Например, следующие перестановки на множестве 3-х первых цифр римской системы счисления {I, V, X} отличаются транспозицией подчеркнутых смежных элементов:Пт: (I) ; (V) ; (X) ; (I) ; (V) ; (VIX)Транспозитивная последовательность легко выстраивается по следующему рекурсивному правилу. Пусть уже имеется последовательность (n-1)! перестановок из (n-1) элементов, в которой соседние перестановки отличаются транспозицией смежных элементов. Каждую из этих перестановок можно расширить до n-перестановки, добавляя элемент n на каждую позицию справа-налево для нечетных по номеру (n-1) перестановок и слева-направо для четных по номеру (n-1) перестановок. Порядок порождаемых таким образом перестановок для 3-х первых целых чисел показан на следующей диаграмме:П3:(123)1 (132)2 (312)3 (321)4 (231)5 (213)6- |^| |^|- справо-налево слева-направо- П2:(12)1<-3 : добавить : 3-> (21)2- нечетно четно- |^|- П1(1)1 <-2: добавить справа-налево- нечетноИз этой диаграммы должно быть понятно, что сначала из тривиальной 1-ой перестановки (1) добавлением справа-налево элемента 2 порождается последовательность 2-перестановок П2, содержащая перестановки (12) и (21). Затем в них добавляется элемент 3, соответственно справа-налево, чтобы получить в итоге желаемую последовательность П3, которая состоит из следующих 3-перестановок:П3:(1 2 3); (1 3 2); (3 1 2); (3 2 1); (2 3 1); (2 1 3)

4,4(32 оценок)

Это интересно:

Здоровье

15.05.2020

Угревые струпья: как расправиться с ними быстро и эффективно?...

14.02.2020

Как быть честным(ой)?...

Компьютеры-и-электроника

03.09.2020

Как стать специалистом в Microsoft Excel: советы от эксперта...

Здоровье

14.05.2022