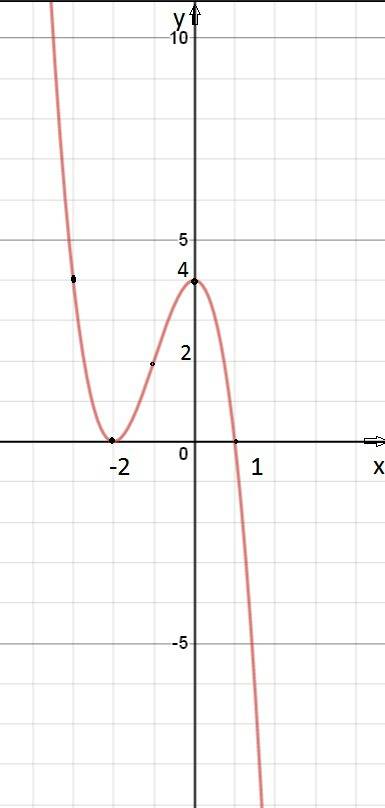
Общий вид уравнения касательной к графику функции у = f(x) в точке х = х0 имеет вид
у = f'(x0)(x - x0) + f(x0).
Найдем уравнение производной f'(x) для функции f(x) = x^3 - 10x^2 + 1
f'(x) = 3x^2 - 10*2x + 0 = 3x^2 - 20x.
Здесь ^ - знак возведения в степень, * - знак умножения.
Найдем значение производной f'(x) в точке х = х0 = 1
f'(x0) = f'(1) = 3*1^2 - 20*1 = -17.
Найдем значение функции f(x) в точке х = х0 = 1
f(x0) = f(1) = 1^3 - 10*1^2 + 1 = -8.
Подставим в общее уравнеие касательной числовые значения f'(1), x0, f(1)
y = -17(x - 1) - 8, y = -17x + 9.
ответ: у = -17х + 9.
при