Объяснение:
1) Треугольники ABM и CBM
AB=BC (по условию)
BM - общая
∠M=90° (по условию)
Вывод: треугольники равны по катету и гипотенузе
2) Треугольники FDN и NKF
DN=FK (по условию)
FN - общая
∠D=∠K=90° (по условию)
Вывод: треугольники равны по катету и гипотенузе
3) Треугольники SDO и SPO
∠D=∠P=90° (по условию)
SO - общая
∠SOD=∠SOP (по условию)
Вывод: треугольники равны по гипотенузе и острому углу
4) Треугольники RMX и XNR
RX - общая
∠MXR=∠NRX (по условию)
∠M=∠N=90° (по условию)
Вывод: треугольники равны по гипотенузе и острому углу
Треугольники MRT и NXT:
RT=XT (тк ∠MXR=∠NRX (по условию), треугольник RTX - равнобедренный (по свойству))
∠M=∠N=90° (по условию)
Из доказательства пары этого пункта ∠MRX=∠NXR (соотв. элементы равных фигур равны), но ∠MXR=∠NRX (по условию)=> ∠MRT=∠NXT
Вывод: треугольники равны по гипотенузе и острому углу
Пусть, для определённости, d>=c>=b>=a. Тогда всю дробь можно переписать в виде:
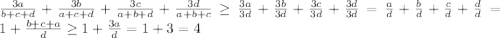
Что и требовалось доказать.
Пояснение: Выражение после первого знака неравенства получается, если взять наименьший знаменатель, а это d+d+d=3d.
Выражение после второго знака неравенства получается оттого, что мы берём наибольший числитель(то есть b+c+a=a+a+a=3a).
Выражение после третьего знака неравенства справедливо так как a>=d, то есть a/d>=1. Отсюда 3*(a/d)>=1*3=3
P.S. Если что-то непонятно, то не стесняйся спрашивать)