Нехай один катет дорівнює х см, тоді другий - дорівнює 0,75х см. Гіпотенуза трикутника становить 12 - (х + 0,75х) = 12 - 1,75х см. За т. Піфагора маємо:
(12 - 1,75х)² = х² + (0,75х)²;
(12 - 1,75х)² - (0,75х)² = х²;
(12 - 1,75х - 0,75x)(12 - 1,75х + 0,75x) = х²;
(12 - 2,5х)(12 - х) = х²;
2,5x² - 42x + 144 = х²;
1,5x² - 42x + 144 = 0;|·(2/3)
x² - 28x + 96 = 0;
x₁ = 24 - не задовольняє умову задачі; x₂ = 4
Отже, один катет дорівнює 4 см, а другий - дорівнює 0,75·4 = 3 см.
Площа трикутника S = 0,5·4·3 = 6 см²
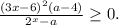ОДЗ: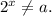 
1-й случай. x=2 - обращает дробь в ноль. Поэтому x=2 является решением при любом a, за исключением случая, когда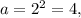 
поскольку в этом случае знаменатель обращается в ноль.
2-й случай.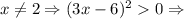 
этот множитель можно отбросить. Получаем
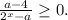
Если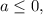 
числитель отрицателен, знаменатель положителен, поэтому дробь отрицательна, и решений нет.
Если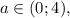 
числитель отрицателен, поэтому для положительности дроби нужно, чтобы знаменатель был отрицателен, 
.
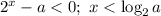Если a=4, дробь равна нулю; x - любой (естественно, за исключением x=2 - об этом мы говорили раньше).
Если a>4, числитель положителен, поэтому для положительности дроби нужно, чтобы знаменатель был положителен,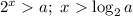 
ответ: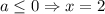 
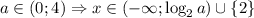
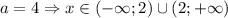
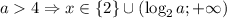
х 0 1
у 0 3 - это ввиде таблицы.
чертеж увы не могу тут рисовать там прямая проходящая через точки!