1) Выделяем полные квадраты:
для y: (y²+2*7y + 72) -1*72 = (y+7)²-49
Преобразуем исходное уравнение:
(y+7)² = 6x - 0
Получили уравнение параболы:
(y - y0)² = 2p(x - x0)
(y+7)² = 2*3(x - 0)
Ветви параболы направлены вправо, вершина расположена в точке (x0, y0), т.е. в точке (0;-7)
Параметр p = -3.
Координаты фокуса: F(-p/2; yo) = (-1,5; -7).
Уравнение директрисы: x = x0 - p/2
x = 0 - 3/2 = -3/2.
2) Выделяем полные квадраты:
для x: (x²-2*1x + 1) -1 = (x-1)²-1
для y: -4(y²+2*3y + 3²2) +4*3² = -4(y+3)²+36
В итоге получаем:
(x-1)²-4(y+3)² = -68
Разделим все выражение на -68
(-1/68)(x - 1)² + (1/17)(y + 3)² = 1.
Параметры кривой.
Данное уравнение определяет гиперболу с центром в точке:
C(1; -3)
и полуосями: a = 2√17, b =√17.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² + b² = 68 + 17 = 85
c = √85.
Тогда эксцентриситет будет равен: e = c/a = √85/2√17.
Асимптотами гиперболы будут прямые: y + 3 = (1/2)(x - 1) и
y + 3 = (-1/2)(x - 1).
Директрисами гиперболы будут прямые: +-е/а = +-(√68/√85).
1. 2)
2. 3)
Объяснение:
1. 
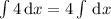, интеграл 
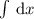табличный и равняется 
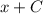, тогда исходный равняется 
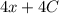, произведение констант — тоже константа, поэтому решением будет 
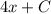, что соответствует второму варианту ответа.
2. Область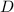 
, ограниченная указанными кривыми 
, 
, 
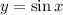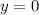и 
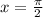, показана на приложенном рисунке. Получается, что 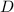задают два неравенства, 
и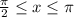 
. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
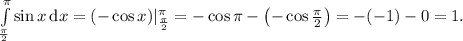
(Так получается, ибо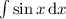 
— табличный интеграл, равный 
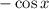, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть 
, при известном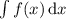 
, то есть 
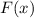, притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.
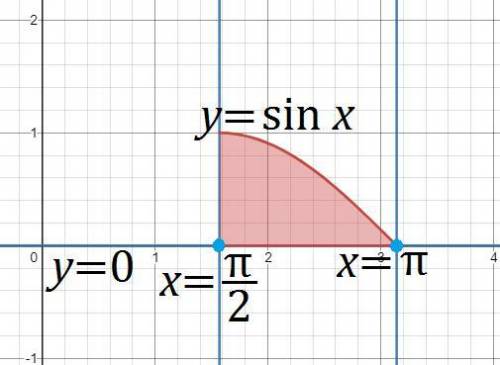
Х^2 -11х +30=0
По теореме Виета
Х1=6 х2=5
(+). (-). (+)
(5)(6)
Х€ [5;6]