
Объяснение:
Добрый вечер.
"Допустимые значения" - это значения, при которых выражение будет иметь смысл.
Для линейных уравнения (это, например, 1 пример 2x-5) подходит любое значение, то-есть от минус бесконечности до плюс бесконечности.
Для второго примера уже не подходит любое значение, ведь на тот же НОЛЬ делить нельзя.
Отсюда и ответ, что любое значение КРОМЕ 0.
В 3 примере примерно тоже самое, знаменатель не должен быть равен 0.
Видите, что в знаменателе Х-5?
Так вот, 0 он будет равен только в том случае, если Х будет равен 5, значит, на место Х можно поступить любое значение КРОМЕ 5.
А в 4 примере так же нет никаких ограничений и 0 тоже можно ставить, ведь ноль делить можно, а вот НА НОЛЬ - нельзя.
ответ - любое значение.
Если что-то не понятно - отпишите в комментариях.
Объяснение:
1) x^2 + (5a-1)x + 4a^2 - a = 0
D = (5a-1)^2 - 4*1(4a^2 - a) = 25a^2-10a+1-16a^2+4a = 9a^2-6a+1 = (3a-1)^2

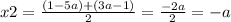
2) Мне кажется, что здесь опечатка, и должно быть так:
x^2 - (2a+3)x + 6a = 0
D = (2a+3)^2 - 4*6a = 4a^2 + 12a + 9 - 24a = 4a^2 - 12a + 9 = (2a-3)^2
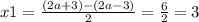
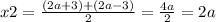
Но, если опечатки нет, тогда так:
x^2 - (2a + 3) + 6a = 0
x^2 - 2a - 3 + 6a = 0
x^2 + 4a - 3 = 0
x^2 = 3 - 4a

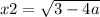
Оба корня существуют, если a ≤ 3/4
3) a^2x^2 - 10ax + 16 = 0
D = 100a^2 - 4*a^2*16 = 100a^2 - 64a^2 = 36a^2 = (6a)^2


Оба корня существуют, если a ≠ 0
4) 3(2a-1)x^2 - 2(a+1)x + 1 = 0
(6a-3)x^2 - (2a+2)x + 1 = 0
D = (2a+2)^2 - 4*(6a-3) = (4a^2 + 8a + 4) - (24a - 12) =
= 4a^2 + 8a + 4 - 24a + 12 = 4a^2 - 16a + 16 = (2a - 4)^2


Оба корня существуют, если a ≠ 1/2