 см, тогда второй катет -
см, тогда второй катет - 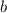 см. Площадь прямоугольного треугольника равна
см. Площадь прямоугольного треугольника равна 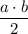 , что составляет 210 см² или перепишем сразу
, что составляет 210 см² или перепишем сразу 
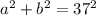
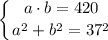
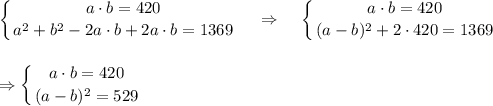
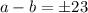 . Тогда имеем несколько случаев.
. Тогда имеем несколько случаев. , то
, то 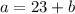 и подставим в первое уравнение.
и подставим в первое уравнение.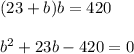
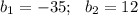 см и корень
см и корень 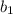 не удовлетворяет заданному условию
не удовлетворяет заданному условию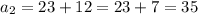 см
см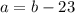 ,то подставив в первое уравнение, получим
,то подставив в первое уравнение, получим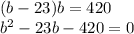
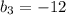
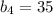 см и корень
см и корень 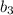 не удовлетворяет условию
не удовлетворяет условию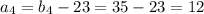
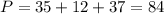 см
см
7-6х-3=10
-6х=10-7+3
-6х=6
х=-1
3)
-5х=-2+9-6
-5х=1
х=-1/5
х=-0.2