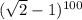раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида 
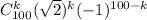по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид 
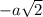, где а - натуральное. Значит, 
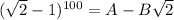, при некоторых натуральных 
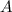и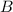 
. (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда 
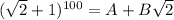, т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим 
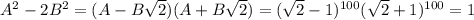, то есть 
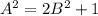. Поэтому, если положим 
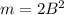, то получим, что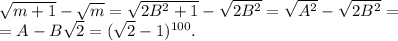 
S = πr² = 3π. Звідси r = √3 см.
Радіус R кола, описаного навколо правильного трикутника, дорівнює 2r,
тобто 2√3 см.
Площа утвореного кільця Sk = πR² - πr² = π(R² - r²) = π(12 - 3) = 9π см².
Для знаходження площі трикутника треба обчислити сторону "а" його:
а = 2rcos 30° = 2√3*(√3/2) = 3 см.
У правильного трикутника висота Н дорівнює сумі (r + R) = √3+2*√3 = 3√3 см.
Площа трикутника St = (1/2)аН = (1/2)*3*(3√3) = (9/2)√3 см².