Объяснение:
Задание 1
а) 5, 10, 15,...; - возрастающая арифметическая прогрессия (d = 5).
б) 3, 0, - 3,...; - убывающая арифметическая прогрессия (d = -3).
г) - 6, - 4, - 2,...; - возрастающая арифметическая прогрессия (d = 2).
д) 11, 9, 7,...; - убывающая арифметическая прогрессия (d = -2).
в) 7, 12, 17,...; - возрастающая арифметическая прогрессия (d = 5).
Задание 2.
d = 2;
a1 = 3, тогда прогрессия такова:
3; 5; 7; 9; 11.
Задание 3.
а) 1, 1, 1, 1, 1, 1, ...;
б) 5, 3, 1, - 1, - 3, - 5, ...
в) - 2, 2, 6, 10, 14, 18,...
В равностороннем треугольнике все стороны равны и каждый угол равен 60°. Также в равностороннем треугольнике все высоты равны, так что найдём любую. Проводим высоты. В равностороннем треугольнике высота является медианой и биссектрисой. Таким образом высота делить сторону длиной
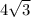
На два равны отрезка. Получим прямоугольный треугольник (так как у гол между сторону и высотой, проведённой к данной стороне равен 90°), у которого катет и гипотенуза равны
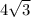
И
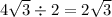
Соответственно, пусть высота равна h, тогда по теореме Пифагора
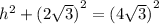
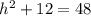
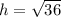
h = 6
ответ: 6
5[x]+27{x}=2012
Комментарии Отметить нарушениеТ. к. 5[x] – целое число и отнимая его от 2012 должны получить тоже целое число 27{x}.
Отнимая от 2012 целое число 27{x} мы должны получить число, которое делится на 5, т. е. кратное 5 ( 5[x] = 2012 - 27{x} ).
При положительных целых значениях 27{x} такое невозможно. Следовательно, решение должно быть дробным.
Подбираем:
1) 2012 – 27х 2/27 =2010;
2) 2012 – 27х 7/27 = 2005;
3) 2012 – 27х 12/27 = 2000;
4) 2012 – 27х 17/27 = 1995;
5) 2012 – 27х 22/27 = 1990.
Других решений не может быть, следовательно, число корней уравнения равно 5.