5х(12х-7)-4х(15х-11)=30+29х
5x(12x-7)-4x(15x-11)-30-29x=0
(5x)(12x-7)-(4x)(15x-11)-30-29x=0
(60x²-35x)-(60x²-44x)-30-29x=0
60x²-35x-60x²+44x-30-29x=0
-20x-30=0
-20x=30
20x=-30
x=(-30):20
x=-1,5
В решении.
Объяснение:
Объяснение:
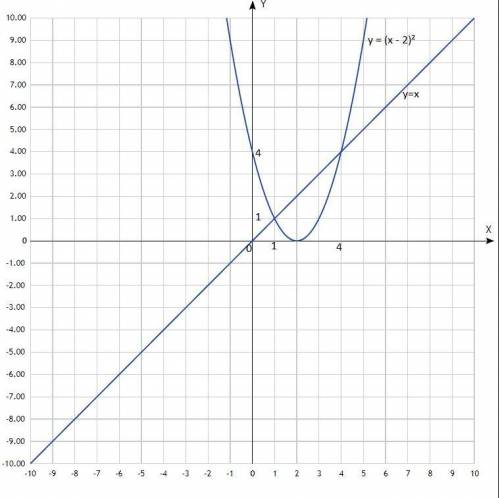
Решить графически систему уравнений:
y = (x - 2)²
y = x
Первый график - парабола со смещённым центром, второй - прямая, проходящая через начало координат.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
y = (x - 2)² y = x
Таблицы:
х -1 0 1 2 3 4 5 х -1 0 1
у 9 4 1 0 1 4 9 у -1 0 1
По вычисленным точкам построить графики.
Согласно построению, координаты точек пересечения: (1; 1); (4; 4).
Решения системы уравнения: (1; 1); (4; 4).
А(0;8) и B(2/3; 7 23/27).
Объяснение:
Дано условие: касательная к функции параллельна оси абсцисс. Из этого следует, что угловой коэффицент k равен нулю, так как k=tgα=tg180°=0, где α - угол наклона между положительным направлением оси абсцисс Ох и касательной, и α = 180°, так как касательная параллельна оси абсцисс.
Нам известно, что k=tgα=f `(x₀), a уравнение касательной к графику функции имеет вид у=kx+c. Зная, что угловой коэффицент равен нулю, получим f `(x₀)=0:
3x₀²-2x₀=0;
x₀(3x₀-2)=0;
(x₀)₁=0; (x₀)₂=2/3
Используя найденные точки, найдём у₀, подставив в формулу уравнения касательной y=f(x₀)+f `(x₀)(x-x₀) или же у-у₀=k(x-x₀), где у₀ - значение функции в точке х₀:
(у₀)₁=f((x₀)₁)=0³+0²+8=8; (у₀)₂=f((x₀)₂)=8/27 - 4/9 + 8= -4/27 + 8= 7 23/27
Преобразовав уравнение касательной у=kx+c в у=с, так как k=0, сделаем вывод, что y функции f(x) 2 касательные: у=8 и у=7 23/27.
Итак, в точках (0;8) и (2/3; 7 23/27) касательные у=8 и у=7 23/27 будут, соответственно, параллельны оси абсцисс.
расскрываем скобки, почленно умножая 5х на то, что в скобках и 4х тоже, на то что в скобках (только не забываем про знак "-")
60Х2 - 35х -60Х2 + 44х = 30+29Х 60Х2 уничтожаются, остаётся
-35Х +44х= 30 +29Х известные в правую сторону, неизв. - в левую
-35Х +44Х -29Х =30
-20Х=30
х=-30/20
Х=-3/2 или -1.5