Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СН = h из вершины С его прямого угла. Она разобьет данный треугольник на два прямоугольных треугольника АСН и ВСН; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС. Все три треугольника АВС, АСН и ВСН подобны между собой. Из подобия треугольников АВС и АСН имеем СН2 = АН×ВН, т.е.
Теорема. Высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна среднему геометрическому отрезков, на которые она разбивает гипотенузу.
h^2=m*n
a^2=c*m
b^2=c*n
c- гипотенуза
m и n - ее части
a) 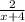
b) 
Объяснение:
Будем раскладывать на множиели при этой формулы :
ax² + bx +c = a(x - x₁)(x - x₂)
a) Для начала нам потребуется найти корни :
x² - x -20 = 0
{ x₁ + x₂ = 1 (система)
{ x₁ × x₂ = -20
x₁ = - 4
x₂ = 5
⇒ x² - x -20 = 1(x - (-4))(x - 5) = (x+4)(x-5)
Теперь подставляем это выражение в знаменатель, а также раскладываем на множители числитель :
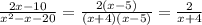
b) Так же, как и в примере, нам нужно найти корни, но уже двух многочленов : (x²+12x+27) и (x²+8x-9).
x² + 12x + 27 = 0
Буду решать через выделение полного квадрата :
(x + 6)² - 9 = 0
(x + 6)² = 9
x+6 = -3 x+6 = 3
x₁ = -9 x₂ = -3
⇒ x² + 12x + 27 = 1(x - (-9))(x - (-3)) = (x+9)(x+3)
Теперь разложим многочлен на множители, который в знаменателе :
x² + 8x - 9 = 0
Решаю опять же через выделение полного квадрата :
(x + 4)² - 25 = 0
(x + 4)² = 25
x+4 = -5 x+4 = 5
x₁ = -9 x₂ = 1
⇒ x² + 8x - 9 = 1(x - (-9))(x - 1) = (x+9)(x-1)
Теперь подставляем эти два выражения :
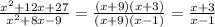
ответ б
2)-4-4x+2=9-15x
-4x-2=9-15x
11x=11
x=1
ответ б
3)б
4)б