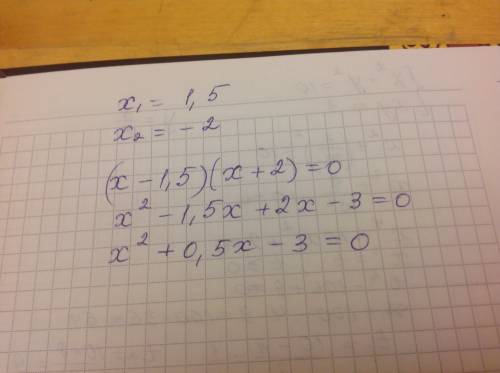
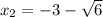
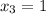
Объяснение:
(x² + 6x)² - 4(x² + 6x + 1) - 17 = 0
t = (x² + 6x)
t² - 4(t + 1) - 17 = 0
t² - 4t - 4 - 17 = 0
t² - 4t - 21 = 0
t² + 3t - 7t - 4 - 17 = 0 (Теорема Виета)
t² + 3t - 7t - 21 = 0
t(t + 3) - 7(t + 3) = 0
(t + 3)(t - 7) = 0
t₁ = -3; t₂ = 7
x² + 6x + 3= 0 x² + 6x - 7 = 0
D = b² - 4ac D = b² - 4ac
D = 6² - 4 * 1 * 3 D = 6² - 4 * 1 * (-7)
D = 36 - 12 D = 36 + 28
D = 24 D = 64
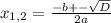
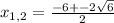
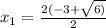
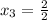
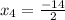
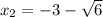
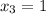
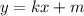: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 
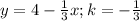. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 
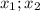, два произвольных числа, но 
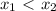. Пусть мы имеем функцию 
, тогда вычисляем значения функции в этих двух точках, имеем 
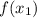и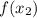 
, так вот, если 
, тогда функция возрастающая, если же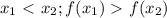 
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
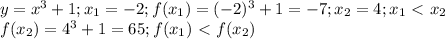, т.е. функция возрастающая. А вот задание с 
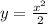не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 
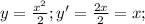. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 
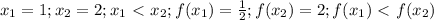, функция возрастает, что и требовалось доказать.
