1) (x-3)(2x-3)+6x² ≥ 2(2x-3)²
Нужно раскрыть скобки2x²-3x-6x+9+6x² ≥ 2(4x²-12x+9)
Если нужно повторяем это действие2x²-3x-6x+9+6x² ≥ 8x²-24x+18
Приводим подобные слагаемые(они подчеркнуты)8х²-9х+9 ≥ 8x²-24x+18
Убираем равные слагаемые(они подчеркнуты)-9х+9 ≥ -24x+18
Переносим х и числа в разные стороны-9х+24x ≥ 18-9
Вычисляем15х ≥ 9
Получаем дробь(х ≥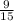
) и сокращаем х ≥ 
или х ≥ 0.6
3) (2х+1)(4х²-2х+1)-8х³≥-2(х+3)
Нужно раскрыть все скобки ((2х+1)(4х²-2х+1) можно упростить используя формулу (a+b)(a²-ab+b²)=a³+b³)8х³+1³-8х³ ≥ -2х-6
Сокращаем противоположные слагаемые(они подчеркнуты)1³ ≥ -2х-6
Переносим х и числа в разные стороны2х ≥ -6 - 1³
Вычисляем2х ≥ -7
Получаем дробь (х ≥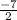
) и выделяем целую частьх ≥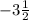 
или х ≥ -3.5
Пусть скорость велосипедиста равна х километров в час. Тогда скорость мотоциклиста равна (х + 15) километров в час. За 2,5 часа мотоциклист проехал:
2,5(х + 15) километров.
За 4 часа велосипедист проехал:
4х километров.
Составим уравнение:
2,5(х + 15) = 4х.
Решим уравнение и найдем неизвестное х:
2,5х + 37,5 = 4х.
1,5х = 37,5.
х = 37,5 : 1,5.
х = 25.
Скорость велосипедиста равна 25 километров в час. Тогда скорость мотоциклиста:
25 + 15 = 40 километров в час.
Расстояние равно:
2,5 * 40 = 100.
ответ: скорость мотоциклиста - 40 км/час, скорость велосипедиста - 25 км/час. Расстояние между городами - 100 километров.
