и 
. Чтобы найти координату 
точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
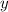можем найти подставив в выражение первой функции , а можно сделать проще. Так как пересечение будет с прямой , то и точки пересечения будут иметь координату . Итак, получилось две точки пересечения с координатами: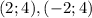 
.![[0;1]](/tpl/images/0561/5883/90495.png)
(этот отрезок по оси ), найдем значения 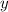на концах этого отрезка: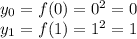
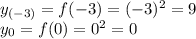
По всей видимости, речь идёт о функции у=-5/(1+х^2)
Если это так, то обратим внимание на то, что знаменатель всегда положителен, поэтому значение функции всегда отрицательное.
Далее, вообще верхний предел этой функции равен 0, при х-> +-бесконечности, поэтому максимальное ЦЕЛОЕ значение, которое может принять функция, равно -1.
Вот в принципе и всё, однако для строгости нужно ещё доказать, что она где-то примет это значение. Это просто, так как мин. значение функции -5 , это очевидно, если глянуть на знаменатель. Поэтому область значений функции [-5;0). -1 входит в этот интервал. Всё.
Ну и последнее. В задаче НЕ ТРЕБУЕТСЯ определить при каком значении х достигается указанный максимум и в общем случае это бывает очень трудно, даже невозможно аналитическими методами сделать. У нас же очень простая функция, поэтому в качестве бонуса определим этот х.
-5/(1+х^2)=-1
x^2 = 4, x=+-2
То есть указанного целочисленного максимума функция принимает даже при двух разных значениях аргумента(хотя это было ясно с самого начала, так как функция чётная).
Вот теперь точно всё.
(-8b³)( -12.5b)(c^5)³=100b^4 c^15