1/2 + корень из 2 cos a, если sin a = корень из 2/2, a принадлежит [90 градусов; 270 градусов]

👇

Ответ:

Gloriyaxx

03.06.2020

Cosa=1-sin^2a под корнем = 1-2/4 под корнем = корень из 2/2
Но т.к. 90-270 градусов - 2-3 четверть, то косинус там отрицательный, т.е.
минус корень из 2/2
корень 2*(-корень из 2/2) = 2/2=1
1/2+1=1,5

4,4(29 оценок)

Открыть все ответы

Ответ:

Sasci

03.06.2020

35.

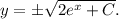
$y = \pm\sqrt{2e^x + C}.$

37.

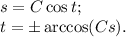
$s = C\cos t;\\t = \pm\arccos (Cs).$

39.

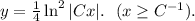
$y = \frac14 \ln^2 |Cx|.\ \ (x \geq C^{-1}).$

Объяснение:

35.

Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. В исходном случае переменные уже разделены, поэтому можно непосредственно проинтегрировать обе части уравнения:

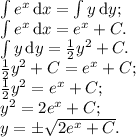
$\int e^x \, \text{d}x = \int y \, \text{d}y;\\\int e^x\, \text{d}x = e^x + C.\\\int y\, \text{d}y = \frac12 y^2 + C.\\\frac12 y^2 + C = e^x + C;\\\frac12 y^2 = e^x + C;\\y^2 = 2e^x + C;\\y = \pm\sqrt{2e^x + C}.$

ответом будет являться найденная функция .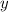

37.

Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. Разделим переменные:

$\text{tg}\, t\, \text{d}t = - \frac{\text{d}s}{s}.$

Теперь можно непосредственно проинтегрировать обе части уравнения:

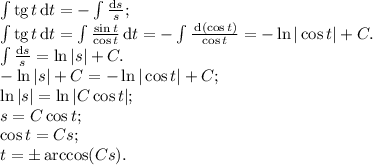
$\int \text{tg}\,t \, \text{d}t = - \int \frac{\text{d}s}{s};\\\int \text{tg}\,t \, \text{d}t = \int \frac{\sin t}{\cos t} \, \text{d}t = - \int \frac{\, \text{d}(\cos t)}{\cos t} = -\ln |\cos t| + C.\\\int \frac{\text{d}s}{s} = \ln |s| + C.\\-\ln |s| + C = -\ln |\cos t| + C;\\\ln |s| = \ln |C\cos t|;\\s = C\cos t;\\\cos t = Cs;\\t = \pm\arccos (Cs).$

Не знаю, что здесь функция, а что переменная, так что в ответе будут в явном виде и s, как если бы переменной была t, и t, как если бы переменной была s.

39.

Данное уравнение — ДУ первой степени первого порядка с разделяющимися переменными. Разделим переменные:

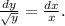
$\frac{dy}{\sqrt y} = \frac{dx}{x}.$

Теперь можно непосредственно проинтегрировать обе части уравнения:

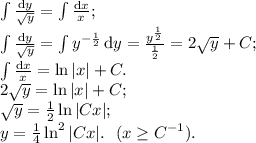
$\int \frac{\text{d}y}{\sqrt y} = \int \frac{\text{d}x}{x};\\\int \frac{\text{d}y}{\sqrt y} = \int y^{-\frac12}\, \text{d}y = \frac{y^\frac12}{\frac12} = 2\sqrt y + C;\\\int \frac{\text{d}x}{x} = \ln|x| + C.\\2\sqrt y = \ln |x| + C;\\\sqrt y = \frac12 \ln|Cx|;\\y = \frac14 \ln^2 |Cx|.\ \ (x \geq C^{-1}).$

ответом будет являться найденная функция 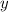с условием.

4,4(89 оценок)

Ответ:

13081990

03.06.2020

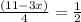1) $\frac{(11-3x)}{4}= \frac{1}{2}$ Умножаешь обе стороны на 4. Сокращается 4 слева и 2 справа. Остается 11-3x=2. Переносишь 2 налево от равно, при этом меняя знак на - . получаешь 11-2-3x=0. И переносишь x вправо от знака равно, также меняя знак с -, на плюс. Получаешь 11-2=3x
9=3x. делишь обе стороны на 3, получаешь x=3

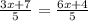2) $\frac{3x+7}{5}= \frac{6x+4}{5}$ . Делаем по тому же принципу что и выше. Умножаем обе стороны на 5, чтобы сократить делитель. Остается 3x+7=6x+4. Меняем стороны, оставляя x c одной стороны, а числа с другой. При смене сторон не забываем менять знаки на противоположные.
Получаем 6x-3x=7-4 отсюда
3x=3 делим на 3 обе стороны и получаем, что x=1

4,5(57 оценок)

Это интересно:

Компьютеры-и-электроника

11.11.2020

Легкий способ - как скопировать музыку с CD в формате MP3...

Компьютеры-и-электроника

17.06.2022

Как установить TortoiseSVN и произвести свои первые изменения в репозитарии...

Компьютеры-и-электроника

19.09.2020

Как распечатать Google Календарь...

Путешествия