ответ: Сумма внешних углов выпуклого многоугольника равна 360°
Объяснение:
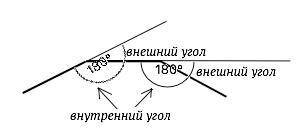
Сумма внешних и внутренних углов любого n-угольника при всех его вершинах равна 180°•n. (т.к. внутренний и внешний угол при одной вершине – смежные и составляют развернутый угол. ) Для нахождения суммы внешних углов из 180°•n вычитается сумма N внутренних углов многоугольника..
Объяснение для 12-угольника.
Сумму внутренних углов выпуклого многоугольника находят по формуле N=180°•(n-2), где N- сумма внутренних углов, n – количество вершин многоугольника. Для треугольника это 180°•(3-2)=180°, для 12-угольника N=180°•(12-2)=1800°.
12•180°= 21600 - сумма всех внутренних и внешних углов 12-угольника, взятых по одному при каждой вершине. Из них на внешние углы приходится 21600°-1800°=360°.
ответ: S = 2 2/3 кв. од .
Объяснение:
y = 0.5x^2 ; y = 2 ;
Рисуємо графіки даних функцій : у = 0,5х² - парабола ;
у = 2 - пряма , паралельна осі Ох .
Заштриховуємо фігуру , обмежену цими лініями : межііетегрування
від - 2 до 2 . Утворена фігура симетрична відносно осі Оу , тому
можна спростити обчислення :
S = ∫₋₂²( 2 - 0,5х²) dx = 2 * ∫₀²( 2 - 0,5х²) dx = 2 * ( 2x - 0,5x³/3)│₀² =
= 2 *( 2x - 1/6 x³)│₀² = 2 * [ ( 2*2 - 1/6 * 2³) - ( 2*0 - 1/6 * 0³) ] = 2( 4 - 4/3 ) =
= 2 2/3 ( кв. од .) .
x∈(-π/3+2πn; π/3+2πn), n∈Z