1. Выпадение 2 очков при 1 бросании = 6, при втором бросании, тоже = 6, значит равновозможных исходов 6*6=36
2. Для того, чтобы 2 очка были наименьшими из выпавших, при первом броске должно выпасть 2, при втором броске - любое количество очков, кроме 1. Или при первом броске - любое, кроме 1, а при втором броске - 2 очка.
3. Возможен вариант выпадения 2 очков и при 1 и при 2 броске, поэтому, при подсчете, вариант это учитывается 2 раза.
3. Выпадение 2 очков из всех, кроме 1 очка = 5, при первом, и 5 при втором броске:
количество благоприятных исходов: 5+5-1=9 ((-1) - выпадение 2 очков в каждом из двух бросаний)
4. Вероятность благоприятного исхода: 9/36=1/4=0.25
ответ: 0.25
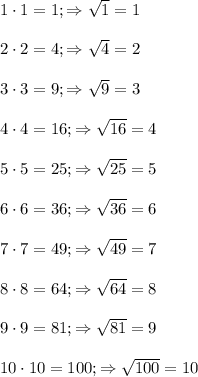
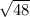и необходимо найти тот промежуток между целыми числами, которому принадлежит данное число. Смотрим в таблицу квадратов. Находим, что 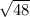находится между 
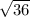и 
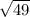, соответственно, 
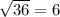, а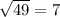 
. Таким образом, 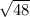лежит между целыми числам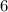и: 
и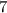 
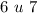
и поставляйте это во второе уравнение
(5 - 3y)^2 + y^2 = 25
25 - 30y + 9y^2 (формула) +y^2 = 25
9y^2 и y^2 подобны
25 -30y + 10y^2=25
с игриком оставляет в левой части, а без игрика переносим
получается 10y^2 - 30y = 0
т.к. 25 из левой переносом вправо со знаком минус
и решаем данное уравнение через дискриминант (проходили ли вы или нет, не знаю)
D= (-30)^2 - 4*10*0= 900 - 0 (т.к. третий множитель 0)
получаем х1=3
х2= -3
теперь поставляе в первое:
3= 5-3у
3у= 5 - 3 (5-х1)
3у=2
отсюда у= 2/3
3у2 = 5-(-3)
3у2= 5+3
3у2= 8
отсюда у2= 8:3 = 2*2/3