Первую ещё не придумала, а вот вторая:
Чтобы найти вероятность того, что точка,брошенная в круг, попадёт в треугольник, надо найти отношение площади правильного треугольника к площади окружности
S(треуг)=(а:2*корень(3))/ S 4
S(окруж)=Pі *r^2
Мы знаем связь между стороной правильного треугольника и радиусом описаной окружности:
r=a/корень3
Тогда, вероятность = S(треуг)/ S(окруж)= ((а:2*корень(3))/ S 4) / (Pі *r^2) = ((а:2*корень(3))/ S 4) * (Pі *а^2) /3=(3*корень3)/ 4Pі
Если надо, можно примерно вищитать:
(3*корень3)/ 4Pі = 3*1,73/4*3,14=5,19/12,56=0,41
ответ:0,41
1. Находим х из 1-го уравнения: х=5+у.
Найденный x подставляем во 2-е уравнение:
(5+у)^2 - 15у=109
25+10у+у^2 -15 у-109=0
у^2-5у-84=0
D=25+336=361
x=(5+-19)/2
x=12, тогда y=7
x=-7, тогда y=-12
ответ: (12;7) и (-7;-12)
2.
x+y=14
x*y=-72
x=14-у
(14-у)у=-72
14у-у^2+72=0
у^2-14у-72=0
D=196-4*1*(-72)=196+288=22^2
у1=14-22/2=-8/2=-4
y2=14+22/2=36/2=18
x1=14+4=18
x2=14-18=-4
ответ: -4 и 18
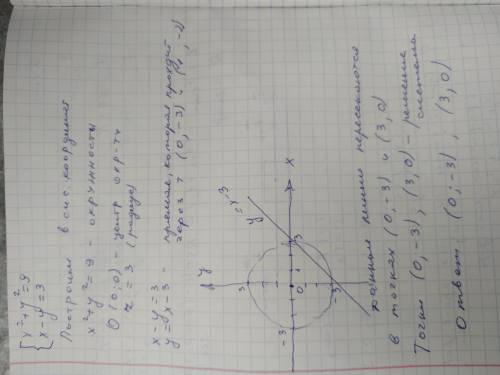
3. Решение в прикрепленном файле:
ответ: (0;-3) (3;0)
4. y=1 / 2 x2 и прямой y=3x-4
1/2x2=3x-4
x2-6x+8=0
D=36-32=4
x12=(6+-2)/2=4 2
x=4
y=8
x=2
y=2
Г80
-Г72
Г0,04*12y
Гa^4*19
Г