Всего 3 + 6 = 9 шаров.
а) Посчитаем, сколько существует взять два белых шара. На каждый из трёх шаров (3 варианта) приходится другой из оставшихся двух (2 варианта). Но так как порядок вытаскивания шаров не имеет значения, то, умножив 3 на 2, мы получим комбинаций двух шаров, учитывая их порядок, т.е. АБ и БА будут двумя разными делим на 2 и получаем один это просто А и Б. Аналогично необходимо поделить на 2 произведение 3 и 2.
взять два белых шара. Проверить данный можно методом подбора, назовём шары А, Б и В. Мы можем взять два шара следующими АБ, АВ, БВ. Их три, убедились.
Аналогично решим с чёрными шарами.
Посчитаем, сколько существует взять два белых шара. На каждый из шести шаров (6 вариантов) приходится другой из оставшихся пяти (5 варианта). Но так как порядок вытаскивания шаров не имеет значения, то, умножив 6 на 5, мы получим комбинаций двух шаров, учитывая их порядок, т.е. АБ и БА будут двумя разными делим на 2 и получаем один это просто А и Б. Аналогично необходимо поделить на 2 произведение 6 и 5.
Здесь подбором долго подбирать, поэтому нужно знать логику решения, описанную выше.
Теперь узнаем общее кол-во взять два любых шара. Логика та же:
Теперь узнаем вероятность того, что два шара, вытащенные из урны одновременно, одинакового цвета. Для этого две первые суммы (3 и 15) поделим на общее кол-во
(15 + 3) / 36 = 18 / 36 = 1/2.
б) В пункте А мы узнали вероятность события А - 1/2. Так как события А и Б - несовместные (если вытащили шары одного цвета, то они не разных цветов, т.е. события А и Б не могут произойти одновременно), значит вероятность события Б = 1 - 1/2 = 1/2.
1/2 = 1/2 ⇒ события А и Б - равновозможные.
Если интересно, как получить вероятность события "шары разных цветов":
На каждый из чёрных шаров (3) приходится по 6 вариантов белых (6). То есть если взять какой-то из чёрных шаров, то будет 6 вариантов для составления комбинации с белым. Поэтому 3 умножаем на 6.
В значении вероятности события Б тоже можно убедиться:
Р(Б) = 18/36 = 1/2
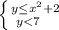
Нарисуем параболу у=х²+2, ветви вверх, вершина в точке (0,2) . Надо заштриховать область, расположенную ниже этой параболы.
Нарисуем прямую у=7, она проходит параллельно оси ОХ через точку (0,7) . Надо заштриховать область, расположенную ниже этой прямой. Так как неравенство у<7 строгое, то линия у=7 не входит в область, её рисуем штриховой линией.
Тогда область, соответствующая системе неравенств, будет та, которая получается в результате наложения штриховок. Верхняя граница этой области обведена зелёной линией.
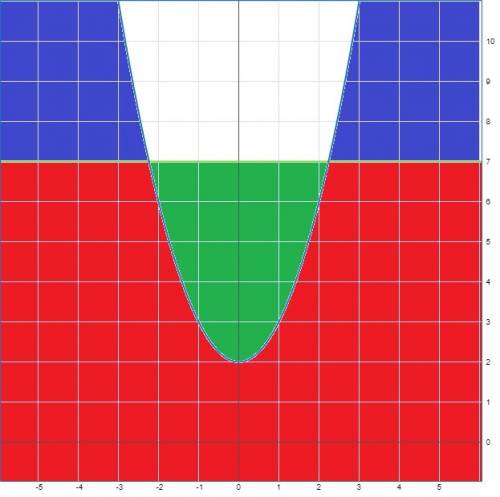
Попробуем повыделять полные квадраты:
Так как квадрат чего-либо всегда неотрицателен, выражение в скобках не меньше 92/25 = 3,68. Значит, максимально возможное значение всего выражения равно -3,68. Оно достигается, если каждый квадрат равен нулю. Посмотрим, возможна ли эта ситуация:
Раз существуют такие y и z, то максимальное значение достигается.
ответ: -3,68