Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
Объяснение:
1) представьте систему в матричной форме
2) умножьте строку 1на (-2) и прибавить результат к строке 2
Умножьте строку 1на (-1) и прибавить результат к строке 3:
3) умножьте вторую строку на -1
4) умножить строку 3 на 2 и прибавить результат к строке 1.
Умножьте строку 3 на 5 и прибавьте результат к строке 2
5) разделить строку 2 на 14
6) умножить строку 2 на -7 и прибавить результат к строке 1.
Умножить строку 2 на -2 и прибавить результат к строке 3
7) умножить строку 3 на -1
8) преобразовать расширенную матрицу систему линейных уравнений
ответ: решение систем уравнений является упорядоченная тройка (х,у,z)
Решение на фотке

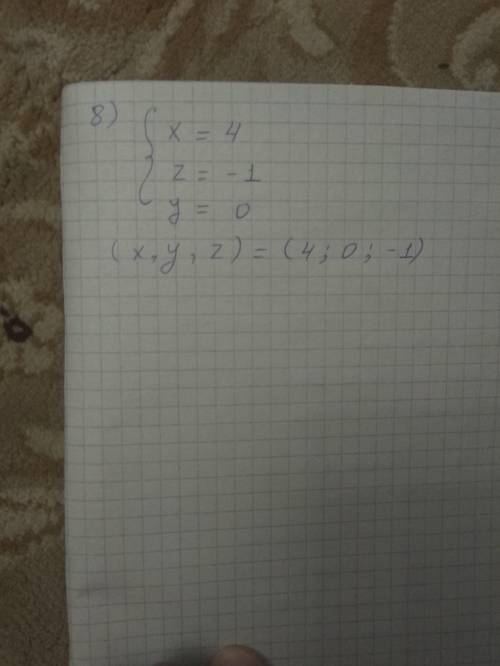
а если ((xy-y^2)/8)*(15/(x-y)) = (y(x-y)/8)*(15/(x-y))=15y/8=15