Перепишем первое уравнение в виде: x + y = -3
Система теперь выглядит так:
x + y = -3
x² + y² = 5
Это чисто метод замены переменной. Пусть x + y = a, xy = b.
Выразим x² + y² через a и b.
(x + y)² = x² + 2xy + y², с учётом замены
a² = x² + 2b + y², откуда
x² + y² = a² - 2b.
Идём далее, с учётом замены перепишем уже систему в следующем виде:
a = -3 a = -3 a = -3
a² - 2b = 5 2b = a² - 5 = 9 - 5 = 4 b = 2
Возвращаемся к старым переменным, учитывая, что x + y = a, xy = b
x + y = -3 y = -3 - x
xy = 2 x(-3-x) = 2 (1)
(1)-3x - x² = 2
x² + 3x + 2 = 0
x1 = -2; x2 = -1
Приходим к двум вариантам:
x = -2 или x = -1
y = -1 y = -2
Система решена



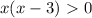
 ∈
∈ 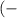 ∞
∞  ∪
∪ 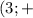 ∞
∞ 

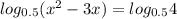
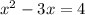
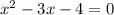
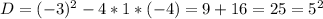
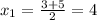
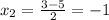



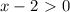
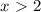
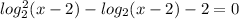

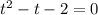

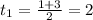

 или
или 
 или
или 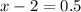
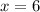 или
или 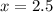

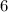
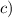
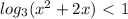

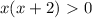
 ∈
∈ 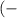 ∞
∞  ∪
∪ 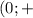 ∞
∞ 

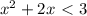


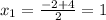

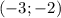 ∪
∪ 
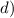
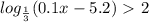







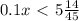



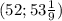
-10sin^2(x) = - 52
sin^2x = 5.2
не попадает под область определения sin(x) = (-1;1)
B)сделаю замену, чтобы меньше было печатать 2x/7 = t
sin2^t - 2sintcost - 3 cos^2t = 0
вынесем за скобку cos^2(t)
cos^2(t) *( sin^2(t)/cos^2(t) - 2sin(t)cos(t) / cos^2t - 3) = 0
cos^2(t) *( tg^2(t)- 2tg(t)- 3) = 0
разбиваем задачу на два случая
1) cos^t = 0
t = Pi/2 + Pi*n где n принадлежит Z
2x/7 = Pi/2 + Pi*n
x = 7Pi/4 + 7Pi*n/2 где n принадлежит Z
2) ( tg^2(t)- 2tg(t)- 3) = 0
cделаем замену tg(t) = y
y^2 - 2y - 3 = 0
y1 = -1
y2 = 3
tg(t) = -1
t = - arctg(1) + Pi*n
t = -Pi/4 + Pi*n
2x/7 = -Pi/4 + Pi*n
x = -7*PI/8 + 7Pi*n/2
tg(t) = -3
t = -arctg(3) + Pi*n
2x/7 = -arctg(3) + Pi*n
x = -7/2 * arctg(3) + 7Pi*n/2