S=4,5 кв.единиц
Объяснение:
Определим точки пересечения заданных линий:
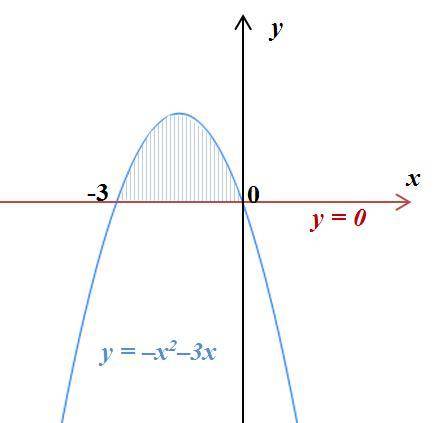
y₁= -x² -3·x, y₂=0
Для этого приравниваем функции
y₁=y₂ ⇔ -x² -3·x=0 ⇔ x²+3·x=0 ⇔ x·(x+3)=0 ⇔ x₁= -3, x₂=0
График функции y₁= -x² -3·x на отрезке [-3; 0] расположена выше графика функции y₂=0 (см. рисунок). Поэтому площадь фигуры определяется следующим интегралом:
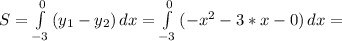
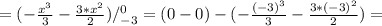
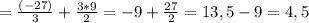
Пусть х км/ч скорость катера, тогда скорость водного мотцикла х+6 км/ч. Время катера в пути 36/х часов, время водного мотоцикла 36/(х+6) часов. Время катера на 1/2 часа больше, чем время водного мотоцикла. Составим и решим уравнение:
36/х - 1/2 = 36/(х+6)
Все переносим в левую часть и приводим к общему знаменателю, получаем вот что:
(-x²-6x+432)/(2x(x+6)) ОДЗ: х≠0, -6
решаем квадратное уравнение, умножив его на мину один:
х²+6х-432=0
D= 36+ 1728=1764=42²
корни этого уравнения: 18 и -24 (-24 не подходит по смыслу задачи)
Значит 18 км/ч, скорость катера, тогда скорость водного мотоцикла 18+6=24 км/ч
ответ: 18 км/ч и 24 км/ч
Объяснение:
Решение - в прикрепленном файле: