![\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}+\dfrac{4}{9\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}}+\dfrac{2}{3}](/tpl/images/1351/8334/f1fa1.png)
Объяснение:
Найдем дискриминант кубического уравнения:
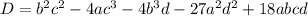
У нас:
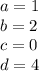
Теперь это нужно посчитать:
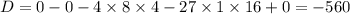
Поскольку D<0, то уравнение имеет 1 вещественный корень.
Выделим полный куб из выражения.
Предварительно вспомним, что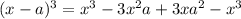 
.
У нас:
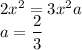
Тогда, учитывая, что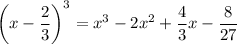 
, получим:
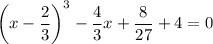
А теперь вынесем 4/3 за скобки:
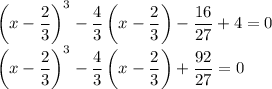
Теперь можно делать замену вида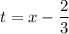 
.
Получим:
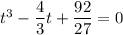
Мы привели уравнение к виду, где отсутствует член со 2-ой степенью неизвестного. Первый этап выполнен.
Второй этап будет заключаться в сведении полученного уравнения к квадратному.
Выполним новую замену:
![t=\sqrt[3]{q}+\dfrac{4}{9\sqrt[3]{q}}](/tpl/images/1351/8334/d6860.png)
Тогда получим:
![\left(\sqrt[3]{q}+\dfrac{4}{9\sqrt[3]{q}}\right)^3-\dfrac{4}{3}\left(\sqrt[3]{q}+\dfrac{4}{9\sqrt[3]{q}}\right)+\dfrac{92}{27}=0](/tpl/images/1351/8334/c3a6d.png)
Посчитав это получим:
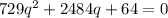
Решив это уравнение через дискриминант получим:
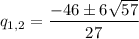
Берем один любой q.
Я возьму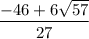 
.
Выполним обратную замену:
![t=\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}+\dfrac{4}{9\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}}](/tpl/images/1351/8334/f60fb.png)
Выполним вторую обратную замену:
![x=\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}+\dfrac{4}{9\sqrt[3]{\dfrac{-46+6\sqrt{57}}{27}}}+\dfrac{2}{3}\approx-1,1304](/tpl/images/1351/8334/f1ebf.png)
Уравнение решено!
Наибольшая прибыль = 7 денежных единиц
Объяснение:
Пусть x - количество произведенной продукции П1, а y - количество произведенной продукции П2. Тогда цель задачи максимизировать значение (
) при условии ограничений на сырье и того, что нам надо произвести хоть что-то: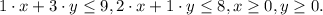 
Эти четыре неравенства задают заштрихованный под прямыми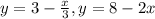 
четырехугольник в первом квадранте.
Значение максимизируемого выражения x+2y есть линии уровня z=x+2y, а так как градиент функции z(x,y) равный grad z = {1;2} направлен в сторону первого квадранта, то значения z будут тем больше, чем дальше мы продвинем линию уровня в первый квадрант. С учетом ограничений наибольшее значение изготовленной продукции придется на пересечение прямых, которые задают четырехугольник: 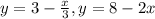. Точка пересечения (3;2). Значит, наибольшая прибыль, которую можно получить 3+2*2=7.
