В решении.
Объяснение:
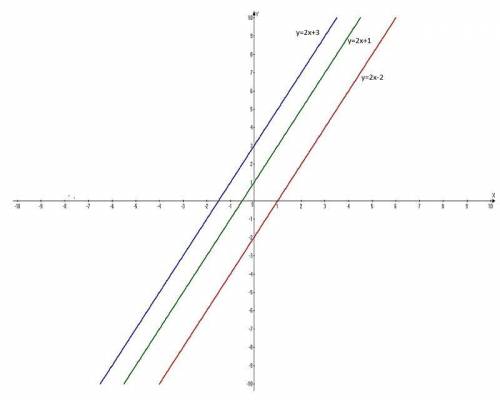
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у = 2х + 1 у = 2х - 2 у = 2х + 3
Таблицы:
х -1 0 1 х -1 0 1 х -1 0 1
у -1 1 3 у -4 -2 0 у 1 3 5
Вывод по построению: графики функций, значения k которых равны (k=2), параллельны друг другу.
Рассмотрим уравнение 2^x +2x =1, сумма возрастающих функций есть возрастающая функция. Справа константа. Значит у данных графиков может быть только одна точка пересечения, что соответствует значению x = 0.
Если решать аналитически, то 2^x = 1-2x. Слева у нас функция >0, возрастает, справа функция убывающая, значит мы не можем рассматривать x, которые >= 1/2, а можем только x <=1/2
Тогда рассмотрим f(x) = 2^x+2x-1 = 0, Найдем f'(x) = 2^x*ln(2)+2, найдем f'(x) = 0, тогда 2^x*ln(2)+2 =0, откуда делаем вывод, что при любых иксах наша функция возрастает, тогда уравнение будет иметь не более одного корня, ведь слева 2^x+2x непрерывна и возрастает для всех значений икс, а справа константа, значит ответ х = 0
∆ ABC,
CK — медиана и биссектриса
Доказать:
∆ ABC — равнобедренный.
Проведем анализ задачи:
На основе каких данных можно утверждать, что треугольник — равнобедренный? Если у него две стороны равны либо два угла равны. Значит, нам нужно доказать либо равенство сторон AC и BC, либо равенство углов A и B. Любое из этих равенств следует из равенства треугольников.
В треугольниках AKC и BKC биссектриса CK образует равные углы ACK и BCK, медиана CK — равные отрезки AK и BK. Сторона CK — общая.
Что мы имеем? Две стороны, но нет угла между ними. Ни к одной из сторон нет двух прилежащих углов. Признаки равенства треугольников применить не можем.
В таком случае придется выполнять дополнительные построения.
На луче CK отложим отрезок KE так, чтобы KE=CK, и точки A и E соединим отрезком. Получили еще один треугольник AKE.
Мы можем доказать, что этот треугольник равен треугольнику BKC (по двум сторонам и углу между ними).
Из равенства этих треугольников следует равенство сторон AE и BC и углов AEK и BCK.
Получается, что в треугольнике ACE имеется два равных угла AEK и ACK. Поэтому он — равнобедренный, откуда легко доказывается и равенство сторон AC и ВС. Осталось записать доказательство.
Доказательство:
На луче CK отложим отрезок KE, KE=CK.
Рассмотрим треугольники AKE и BKC:
1) AK=BK (так как CK — медиана по условию)
2) KE=CK (по построению)
3) ∠AKE=∠BKC (как вертикальные).
Следовательно, ∆ AKE=∆ BKC (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон: AE=BC и соответствующих углов: ∠AEK=∠BCK.
По условию, ∠BCK=∠AСK. Поэтому ∠AEK=∠AСK.
Таким образом получили, что в треугольнике ACE два угла равны. Значит, ∆ ACE — равнобедренный с основанием CE (по признаку). Следовательно, его боковые стороны равны: AE=AC.
А поскольку уже доказали, что AE=BC, то и AС=BС. Поэтому ∆ ABC — равнобедренный с основанием AB (по определению).