Вычислить подробно только log12 3+log12 4 log2√3+ 1/2log2 4/3

👇

Ответ:

хочуха04

11.03.2021

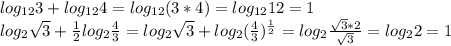
$log_{12}3+log_{12}4=log_{12}(3*4)=log_{12}12=1\\log_2\sqrt{3}+ \frac{1}{2} log_2 \frac{4}{3} =log_2\sqrt{3}+log_2( \frac{4}{3} )^{ \frac{1}{2} }=log_2 \frac{\sqrt3*2}{\sqrt3} =log_22=1$

4,8(28 оценок)

Открыть все ответы

Ответ:

Самозванко

11.03.2021

В решении.

Объяснение:

Моторная лодка против течения реки 308 км и вернулась в пункт отправления , затратив на обратный путь на 3 часа меньше , чем на путь против течения.

Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч .

Формула движения: S=v*t

S - расстояние v - скорость t – время

х - скорость лодки в неподвижной воде.

х + 3 - скорость лодки по течению.

х - 3 - скорость лодки против течения.

308/(х + 3) - время лодки по течению.

308/(х - 3) - время лодки против течения.

Разница во времени 3 часа, уравнение:

308/(х - 3) - 308/(х + 3) = 3

Умножить все части уравнения на (х - 3)(х + 3), чтобы избавиться от дробного выражения:

308*(х + 3) - 308*(х - 3) = 3(х - 3)(х + 3)

308х + 924 - 308х + 924 = 3х² - 27

1848 = 3х² - 27

-3х² = -27 - 1848

-3х² = -1875

х² = -1875/-3

х² = 625

х = √625

х = 25 (км/час) - скорость лодки в неподвижной воде.

Проверка:

308 : 22 = 14 (часов);

308 : 28 = 11 (часов);

14 - 11 = 3 (часа), верно.

4,8(31 оценок)

Ответ:

Akmosh2003

11.03.2021

Для начала, давайте перепишем данное уравнение в более понятной форме:

tg(5x) - tg(3x)/(1 + tg(5x) * tg(3x)) = √3

Для того, чтобы определить все корни этого уравнения, мы будем использовать базовые свойства тригонометрии и алгебры. Давайте разберемся с каждым шагом подробно:

Шаг 1: Упрощение уравнения
Воспользуемся свойствами тригонометрии, чтобы упростить данное уравнение. Заметим, что у нас есть тангенсы с суммами или разностями углов в числителе и знаменателе. Это подсказывает нам использовать формулу тангенса суммы или разности углов:

tg(A ± B) = (tg(A) ± tg(B))/(1 ∓ tg(A)tg(B))

Используя эту формулу, можем переписать уравнение следующим образом:

(tg(5x) - tg(3x))/(1 + tg(5x) * tg(3x)) = √3

Теперь у нас тангенсы находятся в одном выражении в числителе и они относятся к сумме углов.

Шаг 2: Используем общую формулу тригонометрии
Воспользуемся общей формулой тригонометрии, которая связывает тангенс и синус:

tg(x) = sin(x)/cos(x)

Заменим в уравнении тангенсы на их эквивалентные выражения:

(sin(5x)/cos(5x) - sin(3x)/cos(3x))/(1 + sin(5x)/cos(5x) * sin(3x)/cos(3x)) = √3

Шаг 3: Упрощение дроби
Для упрощения дроби, умножим числитель и знаменатель на cos(5x) * cos(3x):

[(sin(5x) * cos(3x) - sin(3x) * cos(5x)) / (cos(5x) * cos(3x))] / [(cos(5x) * cos(3x) + sin(5x) * sin(3x)) / (cos(5x) * cos(3x))]

=(sin(5x) * cos(3x) - sin(3x) * cos(5x)) / (cos(5x) * cos(3x) + sin(5x) * sin(3x))

Теперь у нас получилась дробь с разностями и суммами тригонометрических функций.

Шаг 4: Используем формулу разности тригонометрических функций
Воспользуемся формулой разности тригонометрических функций для упрощения дроби:

sin(A - B) = sin(A) * cos(B) - cos(A) * sin(B)

(sin(5x) * cos(3x) - sin(3x) * cos(5x)) / (cos(5x) * cos(3x) + sin(5x) * sin(3x))

= sin(5x - 3x) / cos(5x + 3x)

= sin(2x) / cos(8x)

Шаг 5: Используем формулу тангенса
Теперь у нас находится отношение синуса и косинуса. Воспользуемся формулой тангенса:

tg(x) = sin(x) / cos(x)

sin(2x) / cos(8x) = tg(2x) * cos(2x) / cos(8x)

= tg(2x) * (2 * cos^2(x) - 1) / (2cos^2(4x) - 1)

Теперь у нас получилось уравнение только с тангенсами и косинусами.

Шаг 6: Подстановка корня
Мы знаем, что tg(x) = √3. Подставим это в наше уравнение:

√3 * (2 * cos^2(x) - 1) / (2cos^2(4x) - 1) = √3

Упростим это уравнение:

2 * cos^2(x) - 1 = 2cos^2(4x) - 1

2cos^2(4x) = 2 * cos^2(x)

cos^2(4x) = cos^2(x)

Шаг 7: Разложение косинуса в квадрат
Воспользуемся формулой разложения косинуса в квадрат:

cos^2(A) = (cos(2A) + 1) / 2

Таким образом, мы можем переписать уравнение:

cos^2(4x) = cos^2(x)

(cos(8x) + 1) / 2 = (cos(2x) + 1) / 2

cos(8x) = cos(2x)

Шаг 8: Решение тригонометрического уравнения
Для решения тригонометрического уравнения cos(A) = cos(B), мы должны рассмотреть два случая:

1) A = B + 2πk, где k - любое целое число
2) A = -B + 2πk, где k - любое целое число

В нашем случае:

8x = 2x + 2πk, или 8x = -2x + 2πk

Для первого случая, мы имеем:

8x - 2x = 2πk

6x = 2πk

x = (2πk) / 6

x = (πk) / 3

Для второго случая, мы имеем:

8x + 2x = 2πk

10x = 2πk

x = (2πk) / 10

x = (πk) / 5

Таким образом, все значения x вида (πk) / 3 и (πk) / 5 являются корнями данного уравнения.

Для окончательного ответа, мы можем записать корни следующим образом:

x = (πk) / 3, где k - целое число
и
x = (πk) / 5, где k - целое число

Это даст нам все корни исходного уравнения tg(5x) - tg(3x)/(1 + tg(5x) * tg(3x)) = √3.

4,4(79 оценок)

Это интересно:

Хобби-и-рукоделие

26.07.2020

Как выращивать спирулину дома...

Питомцы-и-животные

06.06.2020

Как приучить собаку к выгулу: советы от профессионалов...

Стиль-и-уход-за-собой

28.08.2020

Как правильно расчесывать волосы: события волосистой жизни...

Здоровье