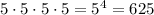Вероятность попадания в мишень одного стрелка при одном выстреле для первого стрелка равна 0.8, для второго стрелка – 0.85. Стрелки произвели по одному выстрелу в мишень. Считая попадание в цель для отдельных стрелков событиями независимыми, найти вероятность события А – ровно одно попадание в цель.
Решение.
Рассмотрим событие A - одно попадание в цель. Возможные варианты наступления этого события следующие:
Попал первый стрелок, второй стрелок промахнулся: P(A/H1)=p1*(1-p2)=0.8*(1-0.85)=0.12
Первый стрелок промахнулся, второй стрелок попал в мишень: P(A/H2)=(1-p1)*p2=(1-0.8)*0.85=0.17
Первый и второй стрелки независимо друг от друга попали в мишень: P(A/H1H2)=p1*p2=0.8*0.85=0.68
Тогда вероятность события А – ровно одно попадание в цель, будет равна: P(A) = 0.12+0.17+0.68 = 0.97
Объяснение:
Нечётных цифр всего 5: 1 , 3 , 5 , 7 , 9 .
1) Надо составить четырёхзначные числа без повторения цифр.
На 1 месте (разряд тысяч) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 2 месте (разряд сотен) можно поставить любую из оставшихся четырёх цифр. То есть это 4 возможности.
На 3 месте (разряд десятков) можно поставить любую из оставшихся трёх цифр. То есть это 3 возможности.
На 4 месте (разряд единиц) можно поставить любую из оставшихся двух цифр. То есть это 4 возможности.
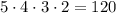
2) Надо составить четырёхзначные числа с возможностью повторения цифр.
На 1 месте (разряд десятков тысяч) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 2 месте (разряд тысяч) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 3 месте (разряд сотен) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
На 4 месте (разряд единиц) можно поставить любую из заданных пяти цифр. То есть это 5 возможностей.
По правилу произведения таких трёхзначных чисел может быть