. Любое число можно представить в виде произведения простых множителей. Запишем:
, где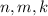 
- некоторые натуральные числа.
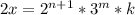является полным квадратом, значит 
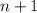и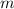 
- четные числа, а 
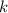- полный квадрат. Аналогично, число 
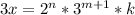является полным кубом, значит 
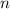и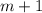 
делятся на 3, а 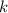- полный куб. 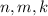это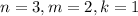 
, значит 
.
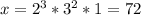в низу
Объяснение:
1. Перетворіть вираз з(ь – 6, 5) у такий, що тотожно дорівнює йому. 2. Запишіть вираз т – (6-n+b) без дужок. 3. Спростіть вираз 15-(a-4). 4. Розкрийте дужки й зведіть подібні доданки у виразі 4b – (76 + 2). 5. Виконайте тотожне перетворення виразу 2,5 (2k + 4а – 2). 6. Спростіть вираз 2(a+1) +а та знайдіть його значення, якщо a=1. 7. Доведіть тотожність (2x +1)-(1-2x) = 4х. 8. Зведіть подібні доданки у виразі -4+32+62. 9. Спростіть вираз -(-5)-(-y). 10. Доведіть, що вираз 7(a-b)+7(b – а) тотожно дорівнює 0. 11. Доведіть тотожність -(2-(-x)+2+x = 0. 12. Доведіть, що сума виразів 13c + 3 і 2c +3 ділиться на
tgx=t
3t-3/t+8=0 ⇔3t²+8t-3=0
t1=[-4-√(16+9)]/3=-3 tgx=-3 x=-arctg3 +πn, n∈Z
t2=[-4+√(16+9)]/3=1/3 tgx=1/3 x=arctg(1/3) +πn, n∈Z
2) sin2x+4cos²x=1
sin2x+2(1+cos2x)=1 sin2x+2cos2x=-1
[1/√(1+4)]sin2x+[2/√5]cos2x=-1/√5
cos(2x-φ)=-1/√5, φ=arctg(1/2)
2.1)2x-φ= (π-arccos(1/√5))+2πn x=[π-arccos(1/√5)+2πn+φ]/2
2.2)2x-φ= -(π-arccos(1/√5))+2πn x=[-π+arccos(1/√5)+2πn+φ]/2
3) 10cos²x-9sin2x=4cos2x-4
5(1+cos2x)-9sin2x-4cos2x=-4
cos2x-9sin2x=9
[1/√(1+81)]cos2x-[9/√82]sin2x=9/√82
cos(2x+φ)=9/√82 , φ=arctg(-9)
3.1)2x+φ= (arccos(9/√82))+2πn x=[arccos(9/√82)+2πn-φ]/2
3.2)2x+φ= -(arccos(9/√82))+2πn x=[arccos(9/√82)+2πn-φ]/2