собственная скорость катера=30км/ч
Объяснение:
48 минут - это 48/60часа=4/5=0,8часа
Пуст собственная скорость теплохода=х, тогда его скорость по течению=х+5. Он потрати времени когда плыл против течения 35/х–5 (поскольку против течения он плыл медленнее), по течению он потратил времени 21/х+5 ( поскольку течение ему и зная что разница во времени составила 0,8часа, составим уравнение:
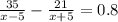
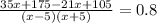
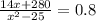
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
(х²–25)0,8=14х+280
0,8х²–20–14х–280=0
0,8х²–14х–300=0
D=b²–4ac=196–4×0,8×(-300)=196+960=1156
х1=(–b+√D)/2a=(14+34)/0,8×2=48/1,6=30
x2=(–b–√D)/2a=(14–34)/1,6= –20/1,6= –5/0,4= –12,5
Итак мы нашли корни и один из них нам не подходит, а именно х2= –12,5, поскольку скорость не может быть отрицательной поэтому мы используем х1=30
ответ:
данные решаются по одному алгоритму.
продемонстрируем на примере первой функции (вторая исследуется аналогично, только функция не определена в точке х=4):
1)
функция не определена в точке x = - 4.
поэтому:
x ∈ (-∞; -4) ∪ (-4; +∞)
2)
находим производную функции:
y'(x) = [(x²+3x)'·(x+4)-(x²+3x)·(x+4)'] / (x+4)²
y'(x) = [(2x+3)·(x+4)-(x²+3x)·1] / (x+4)²
y'(x) = (x²+8x+12) / (x+4)²
3)
приравняем производную к нулю:
x²+8x+12 = 0
x₁ = - 6
x₂ = -2
4)
на интервале x∈(-∞; -6)
y'(x) > 0; функция монотонно возрастает.
на интервале x∈(-6; -4)
y'(x) < 0; функция монотонно убывает.
в точке x = -6 - максимум функции.
y(-6) = - 9
5)
на интервале x∈( -4; -2)
y'(x) < 0; функция монотонно убывает .
на интервале x∈(-2; +∞)
y'(x) > 0; функция монотонно возрастает.
в точке x = - 2 - минимум функции.
y(-2) = -1
6)
для контроля строим график
объяснение: