ответ:1. Вспомним формулы сокращенного умножения.
В нашем выражении присутствует вторая степень. Значит, можно воспользоваться формулами сокращенного умножения со второй степенью:
квадрат суммы: (a + b)^2 = a^2 + 2ab + b^2;
квадрат разности: (a - b)^2 = a^2 - 2ab + b^2;
разность квадратов: a^2 - b^2 = (a - b)*(a + b).
2. Выделим квадрат разности.
Проанализировав выражение, увидим, что 4а^2 - 20аb + 25b^2 похоже на квадрат разности. Определим значения для a и b.
4а^2 - 20аb + 25b^2 = (2a)^2 - 2*(2a)*(5b) + (5b)^2 = (2a - 5b)^2.
Подставим полученный квадрат разности в первоначальное выражение.
(2a - 5b)^2 - 36.
3. Разложим на множители.
Заметим, что 36 = 6^2. Подставим это в выражение.
(2a - 5b)^2 - 6^2.
Теперь мы имеем разность квадратов, где a = 2a - 5b, b = 6.
Подставим эти значения в формулу сокращенного умножения вместо a и b:
((2a - 5b) - 6)*((2a - 5b) + 6);
(2a - 5b - 6)*(2a - 5b + 6).
Следовательно, 4а^2 - 20аb + 25b^2 - 36 = (2a - 5b - 6)*(2a - 5b + 6).
Объяснение:
а) b = 18 б) b = 10 в) y=20 г) y = 1,2
д) a = 9 е) a = 24 ж) x = 1,4 з) x = 0,6
Объяснение:
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции.
a : b = c : d ⇒ ad = bc
а) 2 : 9 = 4 : b; 2b = 9*4; 2b = 36; b = 36 : 2; b = 18;
б) 15 : b = 3 : 2; 15*2 = b*3; 30 = 3b; b = 30 : 3; b = 10;
в) 3 : 2,1 = y : 14; 3 * 14 = 2,1y; 42 = 2,1y; y = 42 : 2,1; y = 20;
г) y : 2,4 = 3 : 6; 6y = 2,4*3; 6y = 7,2; y = 7,2 :6; y = 1,2;
д) 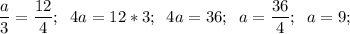
е) 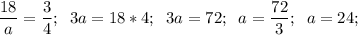
ж) 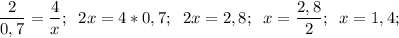
з) 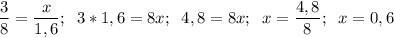
1/x-3>0
1/x>3
0<x<1/3