
x^2=8x-17
x^2-8x+17=0
Д=(-8)^2-4*17=64-68 <0
14x=-49-x^2
X^2+14x+49=0
D=14^2-4*49=196-196=0
x=-14/2=-7
36+17x=-2x^2
2x^2+17x+36=0
D=17^2-4*2*36=289-288=1
x1=-17+1/4=-16/4=-4
x2=-17-1/4=-18/4
7x^2-3x=4
7x^2-3x-4=0
D=-3^2+4*7*4=9+112=121=11^2
x1=3+11/14=1
x2=3-11/14=-8/14
0.81-x^2=0
-x^2=-0.81
x^2=0.81
x=+-0.9
5x+9x^2=0
9x^2+5x=0
x(9x+5)=0
x=0 9x=-5
x=-5/9
1+2x=8x^2
-8x^2+2x+1=0
D=2^2+4*8=4+32=36=6^2
x1=-2+6/-16=-1/4
x2=-2-6/-16=1/2
19x-6x^2-10=0
-6x^2+19x-10=0
D=19^2-4*6*10=361-240=121=11^2
x1=-19+11/-12=-8/-12=2/3
x2=-19-11/-12=2.5
8+2x^2=0
2x^2=-8
x^2=-4 нет корней
40x-25-16x^2=0
-16x^2+40x-25=0
D=40^2-4*16*25=1600-1600=0
x=-40/-32=10/8=5/4
-36-x^2=-12x
-x^2+12x-36=0
D=12^2-4*36=144144=0
x=-12/-2=6
Відповідь:
S10 = 25500
Пояснення:
Випуск продукції це арифметична прогресія з різницею 300.
Використаємо формули для обчислення n члена арифметичної прогресії: an = a1 + d(n - 1)
За 1 місяць виготовлено a1 тарілок, за 2 місяць - a1 + 300, за останній -
a1 + d(n - 1). Складемо систему рівнянь:
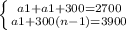
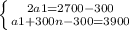
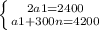
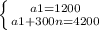
Віднімаємо від 2 рівняння 1 рівняння:
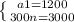
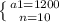
Використаємо формули для обчислення суми n членів арифметичної прогресії: Sn = (2a1 + d(n - 1))/2 * n
S10 = (2 * 1200 + 300 * (10 - 1))/2 * 10 = (2400 + 2700) * 5 = 5100 * 5 = 25500