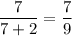V=(40-X)(64-X)X - функция. найти максимум, х∈(0, 40). найдем производную от V=(40-X)(64-X)X=х³-104х²+2560х она равна 3х²-208х+2560 найдем стационарные точки , приравняв производную к 0 , и решив кв. ур-ние 3х²-208х+2560=0 1) х=(104+√(104²-3·64·40))/3=(104+√((8·13)²-3·64·40)))/3= =(104+√(8²(13²-3·40)))/3=(104+8√(13²-3·40))/3=(104+8√(169-120))/3= =(104+8·7)/3=160/3
2) х=(104-√(104²-3·64·40))/3=(104-56)/3=16 ОСТАЛОСЬ по достаточному условию экстремума убедиться, что х=16 - точка максимума, проверяем знаки производной при переходе через эту точку, решаем неравенство 3х²-208х+2560>0, или простыми вычислениями для значений х из соответствующих промежутков.)
Перевод: Числитель дроби на 2 меньше знаменателя . Если эту дробь сложить с обратной ей дробью , то получится 130/63 . Найдите исходную дробь.
Пусть числитель дроби равен х, тогда её знаменатель - (x+2). Обратная ей дробь - (x+2)/x. Составим уравнение согласно условию:
ОДЗ: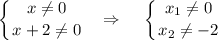
Домножим левую и правую части уравнения на 63x(x+2), получим:
По теореме Виета: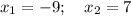
Корни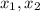 удовлетворяет области допустимых значений.
удовлетворяет области допустимых значений.
Исходная дробь: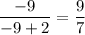 или
или