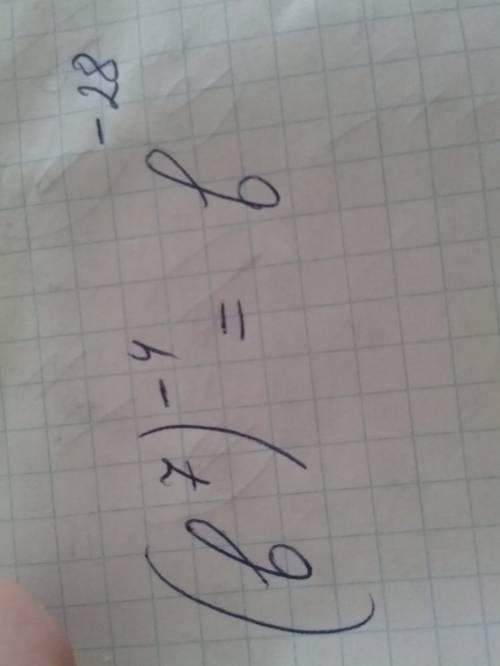
Объяснение:
Выносим общий множитель √2*sinx за скобки
√2*sinx*(2-cosx)+cosx-2=0
Выносим знак минус за скобку
√2*sinx*(2-cosx)-(2-cosx)=0
Выносим за скобку общий множитель 2-cosx
(2-cosx)*(√2*sinx-1)=0
2-cosx=0 или √2*sinx-1=0
1) -cosx=-2 - не существует, поскольку cosx принадлежит [-1:1]
2) √2*sinx=1 делим на √2
sinx= 1/√2
sinx= 1/√2
используем обратную тригонометрическую ф-цию
x=arcsin(1/√2)
sinx периодическая ф-ция добавляем 2Пn, n принадлежит Z
x=arcsin(1/√2)+2Пn, n принадлежит Z
Решаем уравнение
x=п/4+2Пn, n принадлежит Z
Вроде так
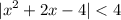
раскроем модуль:
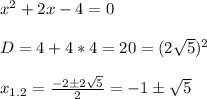
_+___ -1 -√5 ___-___ -1+√5__+__
x²+2x-4 -x²-2x+4 x²+2x-4
1) теперь рассмотрим решение неравенства на промежутках
(-∞; -1-√5] ∪ [-1+√5; +∞)
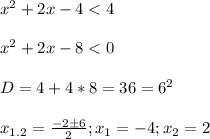
_\\\\\\ -4 _\\\\\ -1-√5_____ -1+√5_\\\\\\_ 2__\\\\\__
////////////////////////////////////////////////
пересечением решений будут промежутки
(-4; -1-√5] ∪ [-1+√5;2)
2) теперь рассмотрим решение неравенства на промежутках
(-1-√5;-1+√5)
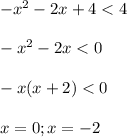
_____ -1-√5_ \\\\\\_ -2_\\\\\\_ 0_\\\\\_-1+√5_____
//////////////////////////// /////////////////////
пересечением решений будут промежутки (-1-√5;-2) ∪ (0; -1+√5)
И Тогда общим ответом будет
(-4; -2) ∪ (0;2)