Пусть эти числа х и х+1(т.к. они последовательные).
Значит квадрат суммы равен: (х+ х+1)²= (2х+1)².
А сумма квадратов равна х² + (х+1)².
Квадрат суммы больше суммы квадратов на 840, значит их разность равна 840 или :(2х+1)² - (х² + (х+1)²)=840 . Раскроем скобки и решим уравнение:
4х² + 4х + 1 - х² - (х+1)²=840;
3х² + 4х -(х+1)² = 840-1;
3х² + 4х - х² -2х -1 = 839;
2х² -2х = 840;
х² - х = 420;
х² - х - 420=0. Квадратное уравнение
D= 1 - 4 * (-420 )= 1 + 1680=1681 = 41²
х₁= 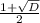 =
= 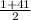 = 21.
= 21.
х₂ < 0 , значит посторонний корень.
Тогда первое число равно 21. а второе 22(т.к. они последовательные)
ответ: 21 и 22.
1. а) 10x - (2x-4)=4(3x-2)
8x+4=12x-8
-4x=-12
x=3
б) 16(0.25х - 1)=5(0.8-3.2)
4х-16=4х-16
4х-4х=-16+16=> уравнение не решается, т.е пустое множество
2. Можно решить уравнением: пусть 1ая сторона-Х, 2ая сторона-(х+6), 3я сторона-(х+9)=>
x+x+6+x+9=33
x=6 - 1ая сторона
6+9=15 - 3я сторона
6+6=12 - 2ая сторона
3. Я не поняла, что такое множество корней, но сами уравнения решила вроде правильно, на всякий случай, проверь:
а) =6х+9х-4х-6-6х^2-2x-18=0
приводим подобные слагаемые, получается: 3х=24; х=8
б) не знаю, правильно-неправильно, но уменя получилось (-1+2/7)- минус одна целая две седьмых
4. Уравнение: 3х+750=х-350; х=200(на первом элеваторе)
200*3=600(на втором элеваторе)
5. при б равном 7 (5х-7=3)
(x^2 - 2x)^2 - (a+2)(x^2 - 2x) + (3a-3) = 0
Замена x^2 - 2x = y
y^2 - (a+2)y + (3a-3) = 0
Если у исходного уравнения 4 корня, то у этого должно быть 2 корня.
При этом у каждого из уравнений x^2 - 2x = y1 и x^2 - 2x = y2 тоже должно быть по 2 корня.
D = (a+2)^2 - 4(3a-3) = a^2 + 4a + 4 - 12a + 12 = a^2 - 8a + 16 = (a-4)^2
При любом а, кроме 4, это уравнение имеет 2 корня.
y1 = (a+2-a+4)/2 = 6/2 = 3
y2 = (a+2+a-4)/2 = (2a-2)/2 = a-1
Обратная замена
1) x^2 - 2x = 3
x^2 - 2x - 3 = 0
(x + 1)(x - 3) = 0
x1 = -1; x2 = 3
2) x^2 - 2x = a-1
x^2 - 2x + 1 - a = 0
D = 4 - 4(1-a) = 4 - 4 + 4a = 4a
x3 = (2 - 2√a)/2 = 1 - √a
x4 = (2 + 2√a)/2 = 1 + √a
При a < 0 корней x3 и x4 вообще нет, то есть всего 2 корня.
При а = 0 будет x3 = x4 = 1, то есть всего 3 корня.
При a > 0, но при a ≠ 4, будет 2 корня x3 и x4.
3) Рассмотрим варианты, когда x3 = x1; x3 = x2; x4 = x1; x4 = x2.
1 - √a = -1; √a = 2; a = 4 - не может быть, тогда уравнение с у имеет 1 корень.
1 - √a = 3; √a = -2 - не может быть, корень арифметический, то есть неотрицательный.
1 + √a = -1; √a = -2 - не может быть, корень арифметический, то есть неотрицательный.
1 + √a = 3; √a = 2; a = 4 - не может быть, тогда уравнение с у имеет 1 корень.
ответ: a ∈ (0; 4) U (4; +oo)
Составим уравнение из условий задачи
n - меньшее натуральное число. Тогда n2 + (n+1)2 + 840 = ( n + n + 1)2
Раскрываем скобки.
Получаем
n2+n2+2n+1 +840 = 4n2+4n+1
или
n 2 + n - 420 = 0
D = b 2 - 4ac = 1681
√D = 41
уравнение имеет два корня n = 20 и n = - 21
Так как n - натуральное, то
ответ n = 20, m = 21