Решите уравнения: а)(х-2)в квадрате+24=(2+3х)в квадрате б)(х+2) в квадрате = 43-6х в) 4(х-1) в квадрате = 12х+3

👇

Ответ:

33даник747

22.11.2021

Х2-4х+4+24=4+12х+9х2
х2-4х+4+24-4-12х-9х2=0
-8х2-16х+24=0
Д=256+768=1024
х1=16+32/-16=-3
х2=16-32/16=1

х2+4х+4-43+6х=0
х2+10х-39=0
Д=100+156=256
х1=-10+16/2=3
х2=-10-16/2=-13

4х2-8х+4-12х-3=0
4х2-20х+1
Д=400-16=384
х1=20+-/384/8
х2=20- -/384/8

4х2 - 4х в квадрате

4,6(31 оценок)

Открыть все ответы

Ответ:

valu49

22.11.2021

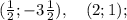
$(\frac{1}{2}; -3\frac{1}{2}), \quad (2; 1);$

Объяснение:

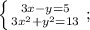
$\left \{ {{3x-y=5} \atop {3x^{2}+y^{2}=13}} \right. ;$

Выражаем из верхнего уравнения переменную "у":

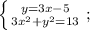
$\left \{ {{y=3x-5} \atop {3x^{2}+y^{2}=13}} \right. ;$

Подставляем полученное выражение в нижнее уравнение вместо "у":

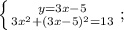
$\left \{ {{y=3x-5} \atop {3x^{2}+(3x-5)^{2}=13}} \right. ;$

Раскрываем квадрат разности двух выражений, пользуясь следующей формулой:

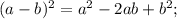
$(a-b)^{2}=a^{2}-2ab+b^{2};$

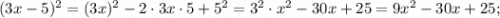
$(3x-5)^{2}=(3x)^{2}-2 \cdot 3x \cdot 5+5^{2}=3^{2} \cdot x^{2}-30x+25=9x^{2}-30x+25;$

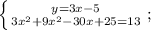
$\left \{ {{y=3x-5} \atop {3x^{2}+9x^{2}-30x+25=13}} \right. ;$

Приведём подобные слагаемые. Для этого вынесем общий множитель за скобки:

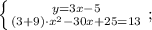
$\left \{ {{y=3x-5} \atop {(3+9) \cdot x^{2}-30x+25=13}} \right. ;$

Выполним сложение в скобке и перенесём слагаемое 13 со знаком минус в левую часть уравнения:

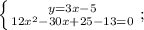
$\left \{ {{y=3x-5} \atop {12x^{2}-30x+25-13=0}} \right. ;$

Выполним вычитание:

$\left \{ {{y=3x-5} \atop {12x^{2}-30x+12=0}} \right. ;$

Разделив все части нижнего уравнения на 6, получим:

$\left \{ {{y=3x-5} \atop {2x^{2}-5x+2=0}} \right. ;$

Теперь разделим все части нижнего уравнения на 2 для того, чтобы получить приведённое квадратное уравнение:

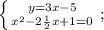
$\left \{ {{y=3x-5} \atop {x^{2}-2\frac{1}{2}x+1=0}} \right. ;$

Решаем нижнее уравнение по теореме Виета. Согласно ей, сумма корней приведённого квадратного уравнения равна коэффициенту при "х", взятому с противоположным знаком, а их произведение — свободному члену:

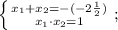
$\left \{ {{x_{1}+x_{2}=-(-2\frac{1}{2})} \atop {x_{1} \cdot x_{2}=1}} \right. ;$

Минус перед скобкой и минус после скобки дают плюс:

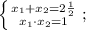
$\left \{ {{x_{1}+x_{2}=2\frac{1}{2}} \atop {x_{1} \cdot x_{2}=1}} \right. ;$

Корнями этой системы являются числа 1/2 и 2.

Мы нашли два значения переменной "х". Теперь подставим каждое из них в верхнее уравнение:

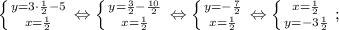
$\left \{ {{y=3 \cdot \frac{1}{2}-5} \atop {x=\frac{1}{2}}} \right. \Leftrightarrow \left \{ {{y=\frac{3}{2}-\frac{10}{2}} \atop {x=\frac{1}{2}}} \right. \Leftrightarrow \left \{ {{y=-\frac{7}{2}} \atop {x=\frac{1}{2}}} \right. \Leftrightarrow \left \{ {{x=\frac{1}{2}} \atop {y=-3\frac{1}{2}}} \right. ;$

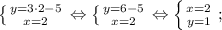
$\left \{ {{y=3 \cdot 2-5} \atop {x=2}} \right. \Leftrightarrow \left \{ {{y=6-5} \atop {x=2}} \right. \Leftrightarrow \left \{ {{x=2} \atop {y=1}} \right. ;$

Мы получили две пары корней:

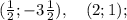
$(\frac{1}{2}; -3\frac{1}{2}), \quad (2; 1);$

Они являются решениями системы.

4,4(15 оценок)

Ответ:

Danila12312

22.11.2021

Будем искать уравнение касательной в виде y-y0=k*(x-x0), где x0 и y0 - неизвестные пока координаты точки касания, k - угловой коэффициент касательной. Но так как k=tg(α), а по условию α=135°, то k=tg(135°)=-1. Теперь уравнение касательной можно записать в виде y-y0=-1*(x-x0). А так как точка касания принадлежит графику функции, то справедливо уравнение y0=5*x0²-2*x0. С другой стороны, k=y'(x0). Производная y'(x)=10*x-2, отсюда k=10*x0-2=-1, или 10*x0=1. Получена система из двух уравнений:

y0=5*x0²-2*x0

10*x0=1

Решая её, находим x0=0,1 и y0=-0,15. Тогда уравнение касательной таково: x-0,1=-1*(y+0,15), или 20*x-2=-20*y-3, или 20*x+20*y+1=0.

ответ: x0=0,1.

4,4(90 оценок)

Это интересно:

Искусство-и-развлечения

19.02.2023

Как прочесть все книги из списка литературы на лето...

Здоровье

28.09.2022

Как прекратить повторение вертиго: причины, симптомы и методы лечения...